看完这些正多边形的尺规作图方法，你还不认为数学也是一种艺术吗？-搜狐

　　荟思

　　正多边形的尺规作图，虽然是一个很纯粹的数学问题，但同时也极具艺术欣赏价值！

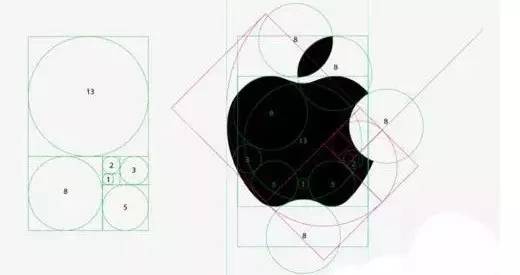
　　尺规作图问题是非常古老的数学问题，早在两千多年前的古希腊时期就开始研究了。人们好奇什么样的图形可以用尺规作图的方法得到，什么样的图形不可以。对于可以尺规作图的图形，很好办，想尽办法得到作图方法就解决问题了。对于那些还没想到作图方法的图形就比较为难，因为不知道是因为不存在这样的作图方法，还是因为作法太复杂，所以还没人能发现这样的方法。例如三等分角问题，就是很长时间里都找不到作图方法，最终证明是不可能办到的。再次特别强调一下，在尺规作图问题中，直尺是不带刻度的，我们只能用它来画直线。

　　在各种图形中，正多边形是大家比较感兴趣的一类。由于圆规可以画圆，而所有正多边形都可以内接于圆，因此它的所有顶点都在圆周上。这样看来，正多边形应该很有希望用尺规作图。而且，前几个正多边形的作图方法很快就构造出来了，步骤也不算复杂。

　　然而还是有很多正多边形没有找到尺规作图的方法，因此自然要问，是否存在不可能尺规作图的正多边形。相对于同时期的其他文明，古希腊数学更富思辨精神。尽管当时的数学问题都是源于生活，但古希腊人并不立足于解决生活问题，而是考虑一般的理想情形。边数较多的多边形在实际问题中几乎不会出现，但他们仍然对这些多边形的尺规作图很感兴趣，并且还执着地规定直尺不能带刻度。

　　这个问题在经过漫长的两千年后，才最终被天才的高斯在24岁时完全解决。根据高斯的结论，一个正多边形可以尺规作图，当且仅当边数是费马素数或者两个不同的费马素数的乘积，或者是这些数的2的乘幂倍（即2倍，4倍，8倍，16倍，等等）。请注意，高斯的结论给出的是一个充分必要条件。换句话说，费马素数的数量决定了能尺规作图的奇数边正多边形的个数。

　　根据高斯的结论，边数不超过20的18个正多边形中，可以尺规作图的一共有11个，边数分别是3,4,5,6,8,10,12,15,16,17,20。不过，高斯的证明只是针对存在性，而没有给出具体的作图方法，包括著名的正十七边形的作法，也不能确定他是否亲自作出来了。

　　下面我们分别来看一下这些多边形的作图过程。

　　正三角形的尺规作图，最简单的方法只需要6步，并且很早的时候就已经被发现了。

　　正方形的尺规作图方法同样简单而且古老。

　　正五边形的尺规作图，在很多书上都能找到。

　　正六边形可以通过对正三角形进一步平分角得到，但下面的方法显然更加简单。

　　正八边形也可以通过对正方形二等分角得到，而下面的作法对这种思路进行了简化。

　　能作正五边形，十边形就能作出来。在得到边的长度以后，用圆规在圆周上画弧的过程真是赏心悦目。

　　正十二边形虽然边数多，但其实比正八边形还好作。

　　正十五边形的尺规作图共需要36步。这个作法也有两千多年的历史了，与正五边形的作法同样出自欧几里得的《几何原本》。确切地说，是第四卷第16题（Proposition XVI of Book IV of Euclid's Elements）。

　　四等分正方形圆心角，即可得正十六边形。

　　关于正十七边形的尺规作图，有一个传说非常动人：19岁的天才数学家高斯一晚上就搞定了悬而未决两千年的尺规作图正十七边形难题，等等等等。但这个说法很可能只是人们善意的谣言，能够确证的说法是名不见经传的Johannes Erchinger在1825年首次解决了这一问题。

　　正二十边形可以通过正十边形得到。

　　相比前面的作图方法，下面我们将要展示的，恐怕更接近于艺术欣赏。

　　叠加正十七边形和正五边形，我们可以轻松得到正85边形。需要注意的是，这招并不总是有效，但可以确定的是，还有51边形和255边形可以使用同样的方法。

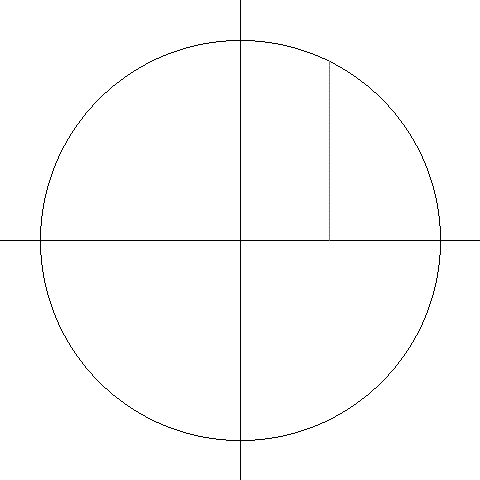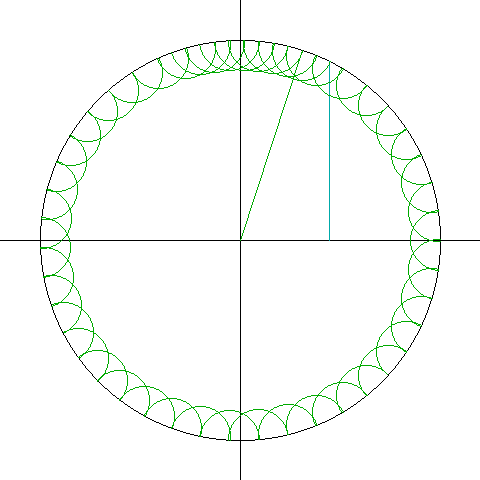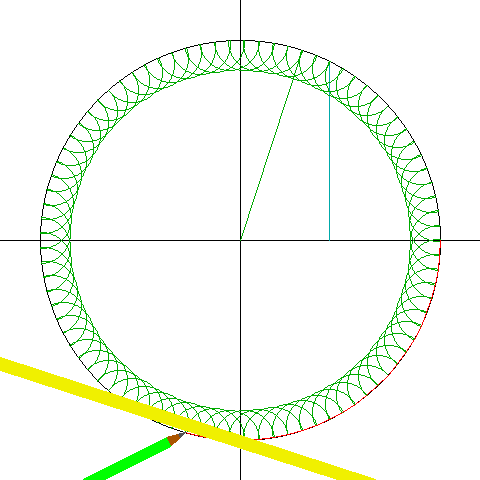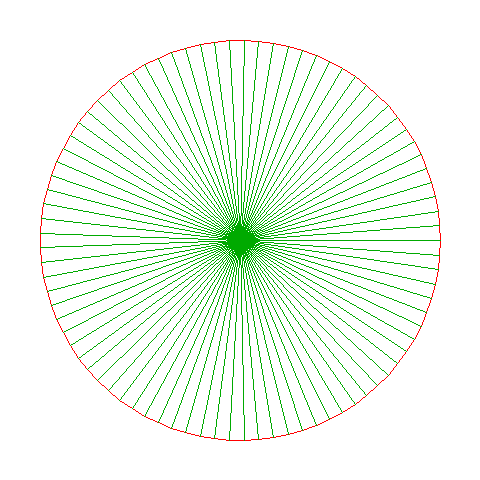
　　叠加正十七边形和正十五边形，可得正255边形——几乎就是个圆。根据高斯的判别法不难想象，当n越大，越少见边数连续分布的可以尺规作图的正n边形，但是255、256、257边形都可以尺规作图。

　　由于257是费马素数，因此正257边形可以尺规作图。1832年Friedrich Julius Richelot和Schwendenwein发表了正257边形利用圆规和尺子绘出的具体方法，除掉将各点连接的步骤，共需要217步。

　　相比前面的尺规作图演示，上面这个257边形的的作图方法可能比较让人纳闷——为什么多边形的外接圆在不断变化？这是因为在作图方法中，如果设定外接圆的半径为1，在作图过程中需要作很多半径比1大得多的圆。

　　高斯的理论表明正65537边形能够尺规作图，但人心都是肉长的，谁都知道如果真的去解决这一难题该是多么摧残身心。可德国数学家Johann Gustav Hermes就是不怕死，他用10年心血解出了正65537边形的尺规作图法并于1894年发表，200多页手稿装了一皮箱，目前保管在哥廷根大学。如果要画出正65537边形及其外接圆，并使边和圆周之间的最大距离为1mm的话，这个圆的半径要超过870公里，实际上这个图画完之后根本看不出那个多边形——画面中央的“小句号”。