数学是宇宙的语言

　　作者：王华平

　　出自线性代数

　　1、上帝是如何创造世界的？

　　毫无疑问，他必然会用简单、优美而又深刻的方程来设计这个宇宙！比如，

　　上帝要求宇宙间所有的星体都要遵从Newton万有引力定律：

　　上帝坚称所有的电磁现象都应该用Maxwell方程进行解释：

　　太阳等几乎所有的恒星之所以能源源不断地辐射热量是因为：

　　宏观低速弱引力场的所有运动大都可以由Newton第二运动定律推导：

　　而以上方程的理论基础就是数学。为了解释、探索自然界的各种现象和奥秘，需要用到物理、化学、生物等科学理论，而这些理论归根结底都要回归到数学。

　　如果大家对以上方程的具体推导感兴趣，有时间的话我会把它们的证明补充完整。

　　早期的物理学家试图找到尽可能多的定律去解释自然界中所观察到的每一现象。而现在的理论物理学家的雄心是，用单个基本定律去取代大量的唯象学定律，以达到对自然的统一描述。物理学家不仅能用电子-光子相互作用理论来解释春天草木的青翠，而且还能用它来解释弹簧的伸长，更不用说激光和晶体管的行为了。事实上，几乎所有我们直接感受到的现象都可以用电子与光子间的相互作用来解释。而这是由规范原理的对称性原理决定的(这种原理遍及整个自然)，其后面的理论基础就是数学。

　　宇宙是简单的，因为所有物质都由原子组成，而原子都是由质子、中子和电子构成，并且所有原子中的质子、中子和电子都是一样的；

　　宇宙是优美的，质子数量的不同导致相异的元素，而中子数量的差异构成同位素，这些丰富的元素和同位素就形成了我们现在缤纷多彩的世界；

　　宇宙是深刻的，要深刻理解原子特别是原子核需要用到量子场论。

　　综上，宇宙是简单、优美而深刻的。下面我们马上就要谈到，数学也是简单、优美而深刻的。因此，上帝选择数学作为宇宙终极设计的语言是非常自然的。

　　2、数学的本质：简单、优美、深刻

　　下面通过微积分和线性代数中的几个方程或公式来阐述数学的简单、优美和深刻！当然，除非你能透彻理解某个公式，不然你很难体会到它的优美。所以，关于数学的优美在此就不多费笔墨了。看看下面这个繁杂的一元三次方程求根式子，

　　你就不难理解以下公式或方程的简洁了。

　　(1) Euler公式：

　　在高中学习三角函数时，很多人都因为要记忆大量的三角函数公式而烦恼过。现在我告诉你，其实只要记住这个Euler公式就可以了，其它的三角函数公式都可以由其推导出来。具体推导容我有时间再更新，敬请期待！

　　这个公式也是Fourier变换的基础，其证明需要用到Talor公式、级数等相关知识。另外非常重要的是：Euler公式的特例

　　将数学中五个极其重要的数

　　联系起来了。五朵“金花”在同一个公式里面绽放，你说它美不美！

　　最后说明一下，Euler的墓碑上刻着的就是这个公式。

　　下面来看看微分学的屠龙刀：

　　(2)Taylor公式：

　　这个公式可以说是计算机和我们人类进行计算的基础，只用纸和笔，我们只能进行加减乘除运算，计算机只能进行加法和移位运算，对于其他的运算就无能为力了，而Taylor公式正好解决了这个问题。学过高数的同学可能发现，还有一个Newton切线法也可以用来进行计算，不过Newton这一方法也是依赖于Taylor公式的。

　　关于Taylor公式，摘录一段话来结束对它的讨论：“我们不想把话说得太绝对，但至少可以说：凡是用一元微积分中的定理、技巧能解决的问题，其中的大部分都可以用Taylor公式来解决。掌握了Taylor定理之后，回过头去再看前面的那些理论，似乎一切都在你的掌握之中，使你有一种‘会当凌绝顶，一览纵山小’的意境，从这个意义上来说，Taylor公式是一元微分学的顶峰并不过分。”

　　接下来出场的是微积分的倚天宝剑：

　　(3)Stokes公式：

　　该公式已经简洁到了极致，而且也异常地优美，更重要的是：它将一元函数的Newton—Lebniz公式、多元函数的Green公式、Gauss公式和Stokes公式全部统一起来了。一元函数的Newton—Lebniz公式又将定积分、不定积分、微分（导数）联系起来了；而多元函数的Green公式、Gauss公式和Stokes公式又将重积分、第一二类曲线积分和曲面积分联系起来了。所以它也是内涵极其深刻的。

　　综上，Stokes公式是简洁、优美而深刻的，是整个微积分中最为重要的公式。并且这个公式也是场论和现代分析的基础。

　　(4)矩阵乘法：

　　线性代数中几乎所有的计算都可以由初等变换来实现，而初等变换只不过是矩阵乘法的逆运算，即左除或右除。很多看似完全不相关的问题，最后都归结为矩阵的乘法。

　　下面来看一下，在线性代数中有哪些问题可以利用矩阵乘法来解决。

计算行列式

求逆矩阵

解线性方程组

解矩阵方程

求矩阵的秩

矩阵的分解

求向量组的秩及其极大线性无关组

判断向量组等价

计算二次型的标准形

计算行列式因子、不变因子、初等因子

求Jordan标准形

求Frobenius标准形

计算特征值

求标准正交基

求过渡矩阵

求多项式的最大公因式

　　这样的简单而又深刻的公式在线性代数和其他数学分支中比比皆是，不再一一列举。最后免费赠送大家几个福利：

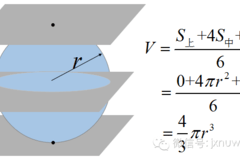
　　(5)体积公式：

　　其中表示用平面去截这个几何体的最上面所得到平面图形的面积。

　　中学里所有几何体的体积都可以由这个公式推导出来。比如，球的体积可以如下推导：

　　

　　(6)链式求导法则：

　　由三大求导法则(链式求导、和式求导、Leibniz求导法则)可以推出三大积分法则(线性积分法、换元积分法、分部积分法)和其他所有的求导法则(对数求导法、隐函数求导法、参数函数求导法、反函数求导法等)。

　　(7)导数公式：

　　利用该公式、Euler公式和链式求导法则可以推导出所有基本初等函数的导数公式。不考虑常数的话，这是唯一一个导数等于其自身的函数。