
“域分解”求解器是一种占用内存较少的迭代算法。利用这一方法,我们可以计算那些无法通过其他直接或迭代方法求解的大型建模问题。此求解器主要在服务器集群上运行,也可在笔记本电脑和工作站中用于求解计算量很大的问题。让我们看看如何在 COMSOL Multiphysics® 软件中使用此功能。
探索 Schwarz 型域分解求解器
“域分解”求解器的原理是将空间域分解为多个相互重叠的子域。相比于求解初始问题,求解子域显得更加简单,同时这种并行的计算方式还能更为有效地利用内存。
为了详细说明迭代空间“域分解”求解器的基本概念,我们采用了一个椭圆型偏微分方程(partial differential equation,简称 PDE)表示域 D,并将域内空间分割为 {Di}i,如此全域便可以被子域 Di的并集完整覆盖,即 D= UiDi。通过这一方法便无需再在全域上求解 PDE,算法只需对每一个子域 Di的若干问题进行迭代求解即可。
在 Schwarz 型域分解方法中,通过子域间相互重叠的部分,即支撑区域来实现子域间的数据传递。在子域之间的界面上,相邻子域的解会被用来更新当前子域的解。举例来说,如果子域 Di与一条边界相邻,那么它会使用此边界条件。为了加速收敛,迭代的域分解过程通常与较粗化网格上的全局求解器(指多重网格中的“粗化求解器”)配合使用。

由正三角形网格构成的二维域,其中域的自由度被分解为二次子域。
在演示如何分解空间域时,我们采用了二维正三角形网格。为简单起见,我们使用了线性有限元形函数,其自由度位于三角形单元的 3 个节点上。域(确切来说是它的自由度)被分解为多个二次子域,每个子域由 25 个自由度组成。所有内部子域均有 8 个相邻子域,且每个自由度与单个子域是一一对应的关系。单个子域中线性单元函数支撑的区域与其相邻子域的支撑区域重叠。
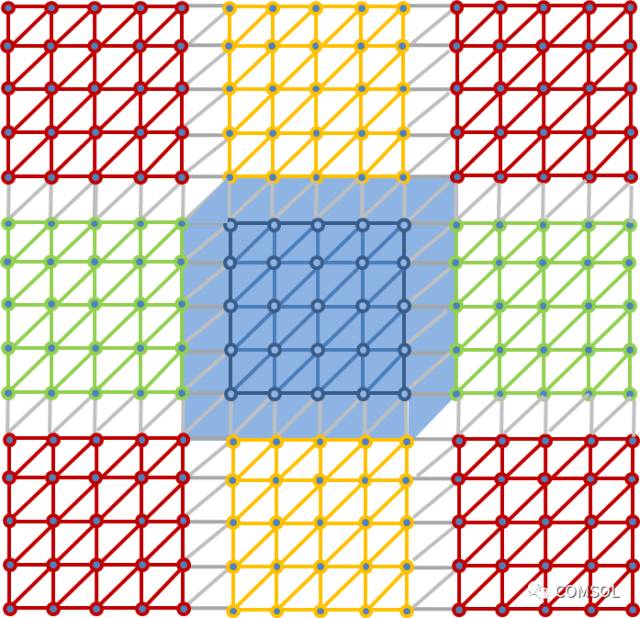
蓝色子域的线性单元函数的支撑区域。
为了提升迭代过程的收敛速度,我们需要引入更多的自由度,用于计算子域间大面积的重叠区域。如此一来,在迭代过程开始收敛之前,子域之间的耦合将变得更加高效,同时迭代次数也会降低。但由于子域面积变大,设置和求解阶段的内存使用量与计算量均会有所增加。
如果需要使额外重叠的宽度增大到 1,可以在现有的子域中额外添加一层自由度。在此案例中,我们向蓝色子域中添加了 22 个自由度(标记为蓝色矩形)。进而相应地增大了蓝色子域的支撑区域。
红、绿、黄三色子域的设置使用了同样的方法。在由此建立起来的子域配置中,一些自由度只属于某一个子域,而其他的自由度可能被两个、三个甚至四个子域共享。很明显,如果一个相邻子域对解进行了更新,被共享的自由度将随之变化。

扩展后拥有 47 个自由度的子域及其支撑区域。相邻子域会共享额外添加的 22 个自由度。
已知(参考文献 1)子域 Di内的子域若干问题的迭代解,会逐渐收敛于全域 D内的原始问题的解。考虑到这一点,我们可以通过以下方式获取全局解:保持其他域不变,单独对每一个子域问题进行反复求解,直到满足收敛标准。粗网格问题的方法能大大提高收敛速度。由于粗网格问题在全域 D中进行求解,因此我们可以通过它大致估计 D内细网格的解。此外,它还能更加迅速地传递全局信息。该方法的收敛速度取决于粗化网格单元的大小与细化网格上重叠区域的宽度之比。
当计算特定的子域 Di时,相邻子域需要对 Di的支撑区域相邻的自由度进行更新。关于如何处理子域重叠域全局粗网格的解,COMSOL Multiphysics 提供了四种方法。在域分解设置中,我们可以将选择器求解器 设置为加法 Schwarz、倍增 Schwarz(默认)、混合 Schwarz 与对称 Schwarz。在加法
Schwarz 方法中,子域之间不发生数据交换,在所有子域计算出全部结果之后,所有受到影响的自由度将同时更新。在这类方法中,子域解的排列顺序是任意的,并且子域在求解阶段相互独立。
倍增 Schwarz 方法与之相反:每个子域的求解完成之后,该方法将对相邻子域的重叠区域内的相关自由度进行更新。这种方式往往能加速迭代求解过程。然而,由于该方法中子域的解不再相互独立,因此我们需要额外指定子域的求解顺序。
至于混合 Schwarz 方法,它会先求解全局求解器的问题,再对解进行更新。随后在同一时刻对子域问题进行求解,这一点与加法 Schwarz 求解器相同。之后,该方法将再一次更新解,并第二次对全局求解器问题进行求解。对称 Schwarz 方法的机制类似于倍增 Schwarz 全局求解器问题求解器,它会按照给定的顺序求解子域问题,只不过将通过对称方式来实现。
直接求解器和预处理迭代求解器
与带有预处理器的迭代求解器相比,直接线性求解器通常更加稳定,且无需过多地调节物理场设置。然而,基于内存方面的考虑,直接求解器无法处理计算量较大的问题。通常情况下,迭代求解器对内存的需求较少,但是由于资源限制,它仍无法对某些模型进行求解。在之前发布的文章中,我们讨论了求解大型模型时的内存需求。由于系统矩阵的具体特性,迭代求解器中的其他预处理器也无法解决此类问题。在很多情况下,域分解预处理器比其他类型的预处理器需要的调节操作更少。
在可用内存有限的情况下,可以将求解过程转移到拥有大量内存的服务器集群。由于“域分解”求解器可以同时执行更多任务,因而我们可以使用域分解预处理器,并根据原始求解器的设置来设定域求解器。正如我们将要看到的,“域分解”求解器也可用于“重新计算并清除”模式,即使在工作站中运行求解器,也能看到内存占用显著降低。
若您不想额外添加粗化网格来构建全局求解器,还可以使用代数方法来进行求解。与“使用粗化级别”的“几何”选项相比,代数方法会增加 GMRES 迭代次数,但其优点在于:它采用最细化级别的系统矩阵来构建全局求解器,而不是通过额外添加较粗化的网格。额外的粗化网格不仅耗费内存,甚至可能根本无法生成;使用了“代数”选项后,我们便可以免去这样麻烦。
在集群上运行域分解预处理
在集群上,我们可在单个节点(或可用节点的单个子集上)上求解子域问题。我们可以通过设置“域分解”求解器来控制子域大小,由此也确定了每个节点占用的内存。加法 Schwarz 求解器能够同时对所有节点上的全部子域问题进行求解。之后在求解器外迭代的最后阶段,对子域界面上的解进行更新。
在倍增 Schwarz 求解器中,子域界面的数据会执行数次中间更新。此方法可以加快迭代过程的收敛速度,但同时会给并行计算引入额外的依赖性。我们必须通过子域染色机制来确定一组可被同时处理的子域。当每种颜色的子域数量很少时,染色的方法可能会限制并行度。总而言之,倍增 Schwarz 和对称 Schwarz 方法的收敛速度比加法 Schwarz 和混合 Schwarz 方法更快,但是后两者的并行加速效果更好。

子域染色机制被用于倍增 Schwarz 型域分解方法的预处理步骤。
在“域分解”求解器的设置中,倍增 Schwarz 和混合 Schwarz 方法都有一个使用求解域染色 复选框。该选项默认为启用状态,主要用于将子域划分为不同的集合(即所谓的颜色)以便对相同的集合进行同时处理。我们选用了一种带有四种颜色的染色方案(蓝、绿、红、黄)。所有相同颜色的子域可同时计算它们的解,并将子域重叠区域上的解传递给相邻子域。因为颜色有四种,所以计算过程重复四次,直到全局解被更新。
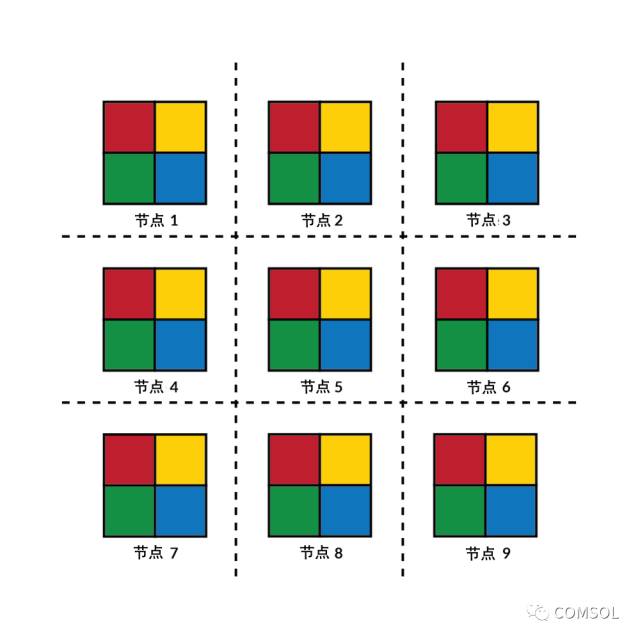
集群上拥有九个节点的域分解。利用子域染色方案,我们可以轮流对每种颜色代表的子域解同时进行计算。
在集群上,子域可以分布在可用的计算节点上。每种颜色均可实现平行处理,所有节点可同时计算当前颜色代表的子域解,当前颜色完成后,便会继续处理下一种颜色。对于倍增 Schwarz 和对称 Schwarz 方法,染色方案能够有效地协调子域的更新顺序。依靠子域之间的信息传递,便能实现计算节点边界上的自由度在不同颜色之间的更新。对于加法 Schwarz 和混合 Schwarz 方法,则不需要对子域进行染色。
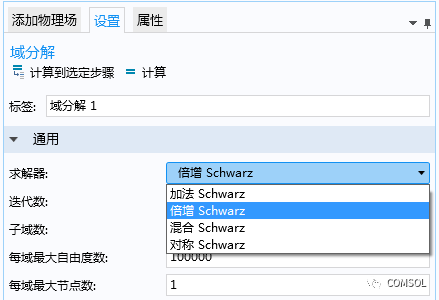
不同的“域分解”求解器类型。
域分解求解器如何处理非分布式情况?
如果“域分解”求解器只在单个工作站中运行,那么全部数据需要在同一个内存空间内进行设置,同时仅存储特定子域的数据并没有太大意义。由于子域发生重叠,因此与原始问题相比,内存消耗甚至可能会增加。为了突破这一限制,我们可以将“域分解”求解器设为在“重新计算并清除”模式下运行,此时每个子域使用的数据可以实现动态计算。很明显,该模式无需将数据存储在虚拟内存中,从而显著降低了内存占用,并能有效求解大型计算问题。由于该过程需要反复重新设置子域问题,因而求解器需要耗费更长时间来完成这些问题的计算工作。
当某个问题的解占用了磁盘交换中的大量虚拟内存时,该方法就非常实用。启用了“自动”选项后,若设置阶段出现了内存不足的错误,“重新计算并清除”功能将会被激活。“重新计算并清除”选项可与直接求解器的“核外”选项媲美。然而两种方法却也都有着其他的弊端:要么是因为在磁盘中存储附加数据(“核外”),要么是因为反复重新计算特定的一部分数据(“重新计算并清除”),导致计算量增加。通过使用“重新计算并清除”选项顶部的无矩阵格式,我们甚至还可以进一步节省更多内存。
调节域分解求解器
在“域分解”求解器的设置中,我们可以对“子域数”(见下图)进行指定。此外,我们还确定了“每个子域的最大自由度数目”。如果遗漏了对最大自由度数,即某一个子域处理的自由度超过了指定数量,那么所有子域将被重新创建,进而导致占用大量子域。
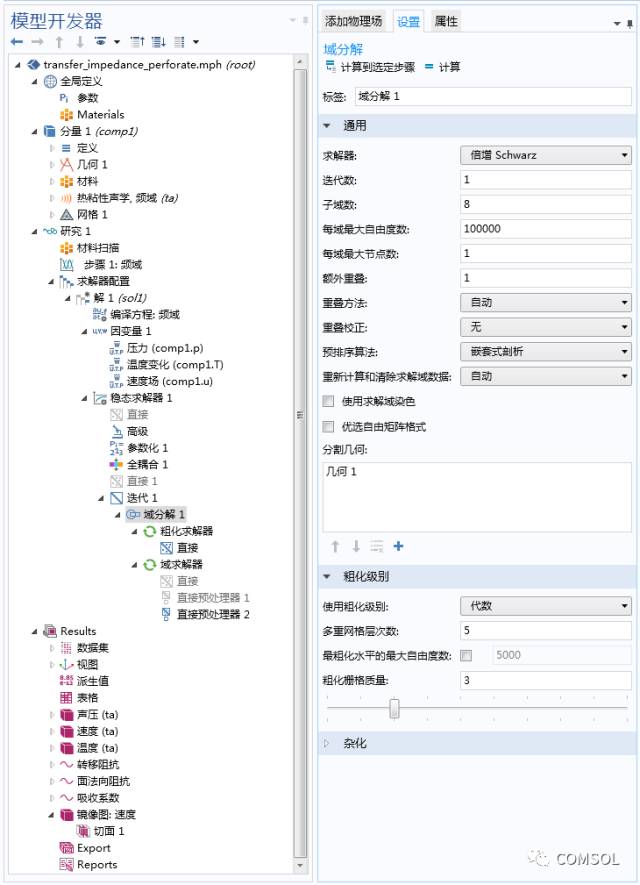
“域分解”求解器的设置窗口。
基于从网格中获取的单元与顶点列表来创建子域。我们可以从数个子域排序方案中选择一种。“嵌套式剖析”选项通过图形剖分来创建子域分布。通常情况下,该选项提供的颜色类型很少,且创建的子域十分均衡,具体表现为自由度数量大致相同、子域界面最小以及重叠区域较小。
另一种可避免域过小的方法是使用基于“空间填充曲线”的“预排序算法”。但是如果启用了“预排序算法”中的“无”选项,子域将按照网格单元和自由度的顺序进行排序,这又会导致生成较小的域。当在“高级”节点中将“求解器”日志设置为“详细”后,求解器日志中将会显示子域配置应用的详细信息。
关于在 COMSOL Multiphysics® 中使用域分解求解器的总结
当在 COMSOL® 软件中模拟需要占用大量内存的问题时,硬件资源往往会成为瓶颈。带有域分解预处理功能的迭代求解器,可以被看作是内存不足时直接求解器的替代品。相应地,在工作站中,“域分解”求解器的“重新计算并清除”选项可被视为直接求解器中内存“核外”机制(即虚拟内存)的替代方案。
尽管内存不足的计算机无法运行内存占用量大的仿真,但是集群可以满足这一需求。COMSOL Multiphysics 的直接求解器可自动使用分布式内存,这一方式有效地降低了每个节点的内存使用量。“域分解”算法求解器是一个附加选项,它的优势在于可以实现以空间域分解为基础的并行计算。
在 COMSOL Multiphysics 中处理大型模型时,本文讨论的“域分解”求解器、集群与各种方法对于提高计算效率十分有帮助。我们将在后续的文章中演示域分解预处理器的具体应用案例。敬请关注!
查看更多关于求解器的资源
查看“COMSOL 博客”中求解器分类下的文章,了解更多有关优化仿真计算方法与内存需求的信息
A. Toselli and O. Widlund, “Domain Decomposition Methods — Algorithms and Theory,” Springer Series in Computational Mathematics, vol. 34, 2005.
本文内容来自 COMSOL 博客
公众号、报刊等转载请联系授权
廉富镯担任执行主编,