1
向你介绍我

大
家好,我是郑维荣,来自绍兴市上虞区丰惠镇小,是朱乐平名师工作站第5组的成员,很高兴能在“一课研究”微信平台上与您相遇!
2
听一听:
整合数学:课程建构新路径
读一读:
整合学习材料,聚焦数学思维
3
整合数学:课程建构新路径
(摘自《小学数学教师》2017第6期)
4
整合学习材料,聚焦数学思维
众所周知,“数学是思维的体操”,而学习材料则是教师教、学生学数学思维的重要载体。毋庸置疑,学生数学思维养成的丰富性和深刻性在很大程度上取决于数学学习材料的好坏。我们可以毫不夸张地说,在某种程度上,课堂教学的成功与否就取决于教师开展教学所用的学习材料。值得欣喜的是,随着课改的不断深化,老师们对学习材料的取舍与利用有了更深层次的思考。笔者以为,将学习材料进行有益整合,学生通过一组或几组整合后的材料的深入研究,探索数学知识,形成数学思维,不失为一种高效的教学方式!现就自身的教学实践与课堂观察,谈一些关于学习材料整合的粗浅想法。抛砖引玉,如有不当之处,敬请专家、同行批评指正。
一、情境材料“一体化”
问题情境拉近了数学与生活的距离,学生通过富有童趣的情境问题的解决,收获知识,形成思想,这正是符合感性有余、理性不足的小学生心智特征的教学方式。然而,当前形势下,为情景而情境、一“步”一 “境”等情境创设方法因其诸多弊端而早已被老师们唾弃。那么,我们的情境教学路在何方?可喜的是,整合问题情境,以情境串的方式串起整节课的教学内容,学生通过解决同一情境下的不同问题,习得新知、丰富思想,已然成为当前数学课堂教学情境创设的一种“新潮”!
如笔者在教学五上年级《用方程解决问题》一课时,就是以自己的家庭成员相关信息为问题情境,串联起整节课的教学(如下图)。课始,课件播放爸爸与小跳的照片,依次呈现爸爸体重、小跳体内水分及成人、儿童体内水分占体重的分值。请生提问、找等量关系,并解决问题。分析得出爸爸体内水分可根据“爸爸的体重×2/3=爸爸体内的水分”直接求得,而小跳的体重则应根据“小跳的体重×4/5=小跳体内的水分”用“12÷4/5=15kg”或用方程解答,引出课题,展开例题教学。然后以线段图的形式出示小跳体重与妈妈体重间的关系。接着根据“爸爸的手长70cm,是身高的5/12”及“爷爷的身高有176cm,妈妈是爷爷的21/22”判断爸爸妈妈谁更高。最后,课件呈现三条关于我们一家三口跳绳成绩的关联信息,让学生推算每人的成绩。尽管课堂中不同问题研究了我们一家人不同的信息,但在教师“猜猜这是谁”“让我们请出小跳妈妈,你知道是老师高呢,还是小跳妈妈高”“你能想办法比较出我们家的跳绳冠军吗”这样富有情趣而又具有挑战性的问题串联下,学生们学得趣味盎然。而这样的教学效果得益于整合的问题情境:整节课,学生一直在研究老师的“私密”信息,而且是一连串的。这样的情境整合与为不同的问题创设不同的情境相比,少却了学生“为做而做”的应付感,增添了“我要研究”的探索味,少却了学生频繁“穿越”情境的生疏感,增添了“深入”问题本质的研究味。真正实现了情境为数学本质服务的创设宗旨。

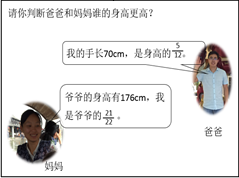
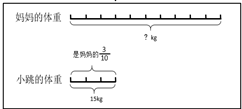

二、探究材料“结构化”
小学生因其“形象思维丰富,抽象思维不足”的思维特征,诸多数学概念、定律、思想的形成往往需要借助一定的探究材料。如学生只有通过对正方体、长方体模型的观察、触摸之后,方能理解正方体、长方体的相关特征;又如只有通过用棱长为1cm的小正方体摆出棱长为1dm的正方体之后,才能掌握1dm3=1000cm3的进率关系,如此种种。可见,探究材料对于学生数学学习而言极其重要!所谓探究材料“结构化”,就是指将一个单元、一节课中各部分的教学内容通盘考虑,设计出一组贯穿各部分内容的探究材料。学生通过对这组材料的不同维度、多方视域的探究,掌握相关数学知识,达成既定教学目标。也就是说,我们应将尽可能多的教学内容落实在尽可能少的学习材料中,让尽可能少的学习材料达成尽可能多的教学目标,实现学习材料的最大化利用。
如全国赛课一等奖获得者王丽兵老师在执教《体积与容积》一课时,就是以一组结构化的学习材料贯穿全课(如下图)。课堂伊始,在学生解读完课本体积与容积相关概念后,教师便呈现这组材料,让学生比较它们的体积大小。通过肉眼比较,学生得出①号纸盒的体积最大;通过数小包纸巾的包数得出两包纸巾的体积分别是第二、第三大。然而土豆和鸡蛋因为它们是不规则的,而大小又非常接近,所以体积无法用肉眼或数的方法进行比较。此时,学生根据科学课中的知识想到了可以用排水法测出体积,比较大小。应当说这组材料的引入不仅让学生理解了体积的意义,更重要的是创设了一个让学生根据问题情境选择合适的测量物体体积的方法(如②、③号纸巾成长方体形状,可以用长的包数乘宽的包数乘高的包数进行计算,如④、⑤号不规则物体可以用排水法测量),为后续体积计算公式的教学作了有效铺垫。但是,教师对这组材料的利用并未就此止步。学生容积意义的理解同样是借助这组材料展开的。因为纸巾、鸡蛋和土豆是实心的,所以它们只有体积没有容积。而纸盒中间是空心的,所以它有容积。学生通过观察,发现这个纸盒的容积和体积就相差在纸板的厚度上。接着,教师拿出正好可以依次嵌入①号纸盒的几个小纸盒,操作后让学生比较纸盒的体积和容积,得出体积不变,容积变小了。在此基础上,教师再拿出正好可以套在①号纸盒外面的纸盒,继续让学生比较,得出容积不变,体积变大了。以此沟通容积与体积间的意义。本课中,王老师提供的这组学习材料,不仅让学生通过对每种材料的研究理解了体积与容积的意义,而且通过将这些材料的重复利用、对比研究、层层递进,无缝连接起了体积与容积间的区别与联系。同时,它还为后续知识的教学作了无形渗透。显然是一组极具结构性的学习材料。

三、训练材料“情节化”
我们反对“题海战术”,但有时一步小心又会陷入“题海”无法自拔。特别是练习课、复习课的教学更容易走上这样的道路。如何推陈出新,让枯燥乏味的练习充满童趣,散发出独特的思辨气息,这是值得每位数学教师深思的问题。笔者在教学实践中发现,将多个训练目标整合于一则材料之中,并为之赋予不同的问题情节,学生通过解答、比较、思辨,实现数学思维的同中求异、异中求同。这样的训练方式学生学得“有味”,教师教得“有劲”。
如有教师在教学《长方体、正方体》单元复习一课时,将一组练习进行有效整合,并为之赋予不同的情节。学生通过用不同的方法解决同一知识点在不同情节中的数学问题,取得了较好的教学效果。在课堂进入练习环节后,教师安排了一题“看我三十六变”的练习题。课件先呈现一个长6dm、宽5dm、高4dm的长方体模型,并依次提出“如果要用角铁制作这个长方体模型,至少需要多少长的角铁?”、“如果这是一个包装箱的模型,那么制作这个包装箱至少需要多少dm2的硬纸板?”、“如果这是一个通风管道的模型,那么制作这样一个通风管至少需要多少dm2的铁皮?”、“如果这是一个玻璃鱼缸的模型,那么制作这样一个鱼缸至少需要多少dm2的玻璃?”、“如果忽略厚度,这个鱼缸能装多少升水?”、“现在鱼缸里水的高度为3dm,如果往里放入一座假山,水面上升到了3.2dm,那么假山的体积是多少dm3?”等问题让学生解答。长方体依旧是那个长方体,但将其置于不同的现实情节之下,我们就不能仅仅依靠原有的表面积、体积计算公式进行求解。学生需要重新调整思路,合理计算。而这样的调整与选择,正是学生数学思维趋向完善的必经之路。讲解中,教师再在题目下方辅以实物图片,让学生“身临其境”理解各种问题情节背后所隐含的“限制”条件。一题多变,让学生在变与不变中,探寻原因、灵活运用、丰满体悟、完善认知。
四、 补充材料“多元化”
“教材无非是个例子”,尽管教材体现着专家、学者们的教学思想与理念,但作为教师的我们,在充分尊重教材的基础上,依旧享有个性化使用教材的权利。特别是当教材中相关学习材料不能很好的与所教班级学生“匹配”时,我们需要补充更接“地气”的材料以帮助学生顺利掌握新知,形成数学思想。此时,多元检索、整合思考,弥足珍贵!
如有教师就将《折线统计图》一课的教学与科学课中的相关知识相结合展开教学的。课始,教师便以变化的数据,引出“蚕宝宝身体长度变化”、“凤仙花植株高度变化”、“我们的身高和体重变化”以及“冰块融化时的温度变化”这四个学生在科学课中深度研究过的例子(如下图),唤醒记忆,激发学生的研究兴趣。接着,以“蚕宝宝身体长度变化”为例,将数据由统计表表示成条形统计图。并以科学作业本中学生所做的“凤仙花植株高度变化统计图”为例(如下图),引出折线统计图,引导学生经历将“蚕宝宝身体长度变化”条形统计图转化成折线统计图的过程,比较两种统计图各自的特征。因为学生材料是学生自己曾经的研究成果,瞬间拉近了知识与学生、旧知与新知之间的联系。让学生在欣赏中发现折线统计图,在对比中感悟两种统计图的特征。而这样的过程又是如此的自然和谐。笔者以为,之所以能取得这样的教学效果,正是基于教师整合课程资源,旁征博引,多元化补充学习材料的教学构想。

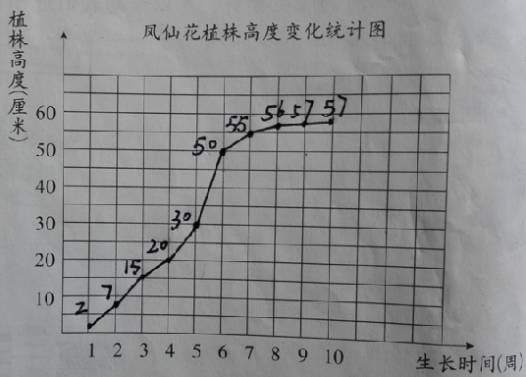
当然,限于能力,以上只是笔者关于整合学习材料的一些粗浅想法。可以想见,学习材料的整合方法还有许多。我们坚信,只要教师以“整合”的眼光审视学习材料,以“树人”的眼光聚焦数学思维,我们的数学教学必将走向深入。


本期审核人:许兆婕 任超琼