
在下面的括号里填上>,<或者=
5()15、12()21、56()65、4+3()10、10-8()4、2+2+3()6、15+2()19-1、10-4()2+2+3、10+3()10-3

下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?
(每座小桥最多只准走一次,陆地上可以重复地来回走)
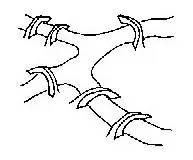

在一条河的中间有两个小岛,周围有六座桥与两岸相通.问能否找到一条路线,从一岸出发,不重复走遍所有的桥,然后到达对岸?

从1、2、3、4、5、6、7、8、9、10这10个数中,任取5个数相加的和与其余5个数相加的和相乘,能得到多少个不同的乘积。

五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时 又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加 的有4人.求这个班的学生人数.

把一个两位数质数写在另一个两位数质数右边,得到一个四位数,它能被这两个质数之和的一半整除,那么这样的两个质数乘积最大是()。
做 完 题 再 看 答 案
养成好习惯

5(<)15、12(<)21、56(<)65、4+3(<)10、10-8(<)4、2+2+3(>)6、15+2(<)19-1、10-4(<)2+2+3、10+3(>)10-3

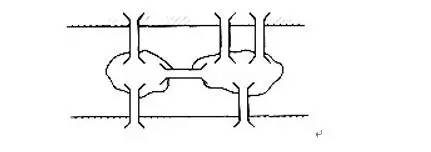
见下两图,可知不能一次不重复地走遍所有的小桥,因为下右图有4个奇点.
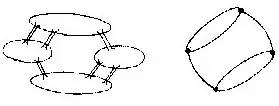

用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,由于此图中有A和C两个奇点,虽然可以一笔画出此图形,但起点和终点必须为A和C,所以要想以C和D分别为起始点和终点,是无法一笔画出此图形的,所以不能找到一条路线,从一岸出发,不重复走遍所有的桥,然后到达对岸.


从整体考虑分两组和不变:1+2+3+4+5+6+7+8+9+10=55 从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55 最接近的两组为27+28 所以共有27-15+1=13个不同的积。
另从15到27的任意一数是可以组合的。

设参加自然兴趣小组的人组成集合A,参加美术兴趣小组的人组成集合日,参加语文兴趣小组的人组成集合C.
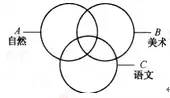
所以,这个班中至少参加一项活动的人有25+35+27-12-8-9+4=62,而这个班每人至少参加一项.即这个班有62人.

根据题意,设出两个质数,再根据题中的数量关系,列出方程,再根据未知数的取值受限,解答即可.
解答:解:设a,b是满足题意的质数,根据一个两位质数写在另一个两位质数后面,得到一个四位数,它能被这两个质数之和的一半整除,
那么有100a+b=k(a+b)÷2( k为大于0的整数),
即(200-k)a=(k-2)b,
由于a,b均为质数,所以k-2可以整除a,200-k可以整除b,
那么设k-2=ma,200-k=mb,( m为整数),
得到m(a+b)=198,
由于a+b可以被2整除,
所以m是99的约数,
可能是1,3,9,11,33,99,
若m=1,a+b=198且为两位数 显然只有99+99 这时a,b不是质数,
若m=3,a+b=66 则 a=13 b=53,
或a=19 b=47,
或a=23 b=43,
或a=29 b=37,
若m=9,a+b=22 则a=11 b=11(舍去),
其他的m值都不存在满足的a,b,
综上a,b实数对有(13,53)(19,47)(23,43)(29,37)共4对,
当两个质数最接近时,乘积最大,
所以两个质数乘积最大是:29×37=1073,
故答案为:1073.

余数问题
基本概念:对任意自然数a、b、q、r,如果使得a÷b=q……r,且0<r<b,那么r叫做a除以b的余数,q叫做a除以b的不完全商。
余数的性质:
①余数小于除数。
②若a、b除以c的余数相同,则c|a-b或c|b-a。
③a与b的和除以c的余数等于a除以c的余数加上b除以c的余数的和除以c的余数。
④a与b的积除以c的余数等于a除以c的余数与b除以c的余数的积除以c的余数。
例:盒乒乓球,每次8个8个地数,10个10个地数,12个12个地数,最后总是剩下3个.这盒乒乓球至少有多少个?
分析与解答:
如果这盒乒乓球少3个的话,8个8个地数,10个10个地数,12个12个的数都正好无剩余,也就是这盒乒乓球减少3个后是8,10,12的公倍数,又要求至少有多少个乒乓球,可以先求出8,10,12的最小公倍数,然后再加上3.
2 8 10 12
2 4 5 6
2 5 3
故8,10,12的最小公倍数是22253=120.所以这盒乒乓球有123个.

声明本文素材来源于网络。以上图文,贵在分享,版权归原作者及原出处所有,内容为作者观点,并不代表本公众号赞同其观点和对其真实性负责。如涉及版权等问题,请及时与我们联系。

