1
向你介绍我是谁
大家好！我是“一课研究”第8小组的学员伊秀君，任教于杭州运河学校。很高兴与您在一课研究的微信中相遇！
2
本期内容有哪些
听一听：估算教学中“数据重塑与算式转换”
读一读：估算教学的困惑和四套教材的比较
想一想：数学小游戏
3
轻轻松松听听书
估算教学中“数据重塑与算式转换”
4
坚持阅读八分钟
人教版教材从二下开始学习估算，但估算这一内容因为存在着方法的多样性和思考过程的复杂性，并未真正融入数学课程，与相关内容以及教师的教和学生的学仍是一种对立关系。这一课程内容在教学实践中存在着很多问题，既难教又难学。
一、直面二年级估算教学中的困惑
新教材在二年级没有给出固定的求近似数的方法，而是让学生充分应用现实情境及数线这个直观模型加以突破，一般情况下求近似数都是求离精确数最接近的整千、整百数。在现实教学中写出一个数的近似数有时与四舍五入相联系，有时根据需要却要违背四舍五入法，特别在估算中经常遇到，这样只能依赖于学生的数感。但完全依赖于学生的数感来教学这块知识，缺少方法的依托，老师和学生都觉得无所适从。
1.数感和经验双缺，新知无法建模
一年级只要把一个数估成整十数，二年级一个准确数的近似数可以是多个，可以估成整千，或是几千几百。怎样让孩子重新建模，只能依托于生活情境，依赖于学生的数感，二年级的孩子处于数感和经验双缺状态，显得很苍白。像下面这样的习题答案是各种各样，教学参考给出的建议是“结合生活情境写出这个数的近似数”，殊不知答案的不唯一容易让学生心理上产生不安全感，学生对“近似数”很是糊涂。
2.估算策略多样，学生拿捏不准
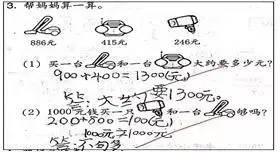
估算策略的选择是受问题情境和问题目标制约的，在不同的问题中，对数据重塑的方式是不一样的。这些因素是导致估算难教、难学的主要原因。如下图一的题目需要“小估”：订书机“886元”估成“800元”，吹风机“246元”估成“200元”，列式：800+200=1000元，1000元=1000元，由此来判定带“1000元”是不够的。下图二的题目却需要进行“大估”，把一年级学生估成“600人”二年级学生估成“600人”，600+600=1200人，1200=1200，所以结论是能坐得下。估算策略的多样性不同于通常解决问题方法的模式化，策略选择的思考中存在着诸多的不确定因素甚至风险，这些都使得二年级孩子在运用估算解决问题的过程中自然出现了“拿不准”的感觉，这种拿不准的感觉就会使学生宁愿使用精确计算，不愿使用估算。
3. 估算过程之繁，学生望而止步
郜舒竹教授在《小学数学这样教》中指出：相对于精确计算，估算具有思维复杂性的特征。要解决“够不够”的问题实际就是比较“318+258”的计算结果与“500”的大小，如果不使用估算，只需直接计算出“318+258”的结果为576；如果要使用估算，要思考的内容就繁琐得多了。
以上对比分析表明，运用估算方法解决问题，从算式的计算程序来看，其强度和难度都有所下降，但从解决问题整体思维的角度看，其含量却大大增加。它需要结合问题情境和问题目标等因素对诸多可能的方法进行列举、比较和筛选，并在此基础山对方法的选择进行判断。因此，学生在解决下列问题的过程中，100%的学生都使用了精确计算，不愿意使用“复杂”的估算。
4.没有约等号的估算，思路难呈现
用来表示两个数近似相等的符号叫做约等号。教材要求二下学生能根据实际情况，运用估算解决实际问题，是“估算”这个知识点的起始教学。起始课的教学却没有出现“约等号”，而是用文字“约、看成”来代替。二年级的孩子，接触数学只有两年时间，回答问题、解决问题都还待规范中。以课本中解答估算的过程，细碎繁琐，没有程序，思维慢的孩子抄都抄不会。老师也很难做规范的示范和讲解，只能要求像以下问题(2)这样解答，但这样的解题步骤学生思路难呈现。
二、了解“生”“本”，为破解困惑奠基
教学应把握好教材的编写意图和教学内容的教育价值，把握好教学内容的数学实质，然后设计一个好的教学方案。笔者研读了四套版本二下的估算教材，并对四套教材中的教学核心要素作了分析比较。
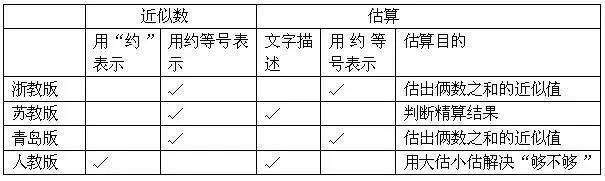
1.浙教版、苏教版、青岛版估出两数之和的近似值，有理有法
从上表中可以看出这三套教材都是按“认识近似数——用估算解决问题（估出两数之和的近似值）”的顺序进行教学的。浙教版、青岛版让学生采取“就近变为整百数”这一习惯的估算策略估出运算结果，强调估算算式的完整性和规范性，认识“≈”和“=”的区别，形成习惯，培养估算意识。苏教版例题呈现求两个年级一共捐了多少本书，先估再精算，也是强调让学生把两个加数看作与之接近的整百数确定精算结果的范围。
这三套教材（见下图）同时让学生运用“就近变为整百数”的估算策略进行估算，教学内容循序渐进，符合学生认知规律；估算过程和估算方法有理有法，学生经历过程明理明法。
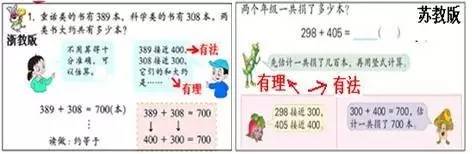
2.人教版用估算解决“够不够”问题有理而无法
人教版教材是按“认识近似数——用估算解决够不够”的编排顺序进行学习的，都没出现约等号。估算例题呈现“分别用500和700元买358元的电话机和218元的吹风机两样东西够不够？”要解决这一问题，“就近变为整百数”这一习惯的估算策略是不能够达成问题目标的，需要学生能根据“问题目标”选择适当的“大估小估”的估算策略。在过程中让学生初步感受估算策略的多样性，同时注重估算策略选择的指导，发挥其培养思维的育人功能。在配套的课作中也注重了估算策略选择培养的练习（下图）。
“大估小估”已偏离了“四舍五入法”。同样的数据在解决“500元够不够”和“700元够不够”两个不同的问题中，对其进行数据重塑的方式也不一样。这样的估算过程，学生明理但无法可效仿，只能是经历过程，积累估算策略选择的经验。
（未完待续）
5
数学小游戏
在一次分数化简的课堂上，珍妮发现分数26/65的分子和分母的6正好可以用一斜线消去，如：
你还知道有哪些形式为ab/bc的数字可以直接消掉b而化简为a/c吗？此题不考虑a＝b＝c的情况。解答
本期审核：何月丰 王嵘