指数分布与餐厅等位时间

　　指数分布（Exponential distribution）是一种连续概率分布，用来预测独立随机事件间的时间间隔。例如客户进入商店的时间间隔，餐厅等位就餐的时间间隔，广告被连续点击的时间间隔，用户重复购买的时间间隔等等。本篇文章通过餐厅等位这件生活中经常出现的事情来说明指数分布的计算方法。

　　下面是指数概率密度函数的计算公式，其中u表示独立事件发生时间间隔的期望值或均值，x表示独立事件发生的时间间隔，f(x)表示独立事件发生时间间隔的概率密度函数。e是自然常数（约为2.71828）

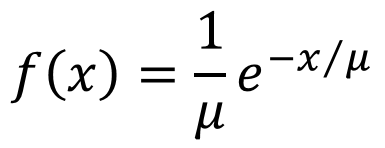
　　除了指数概率密度函数的计算公式以外，还有一个用于描述指数分布的累积概率计算公式，用来表示时间间隔随机变量的值小于或等于某一特定值的累积概率。下面我们通过餐厅等位的时间间隔来具体说明指数分布概率密度函数和累积概率的计算方法。

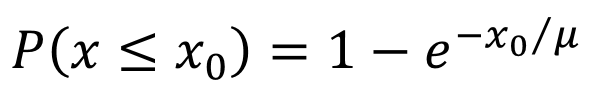
　　假设我们在一家热门餐厅排队等待用餐，并获知该餐厅的平均等位时间为20分钟。那么，这家餐厅等位用餐的概率密度函数是：

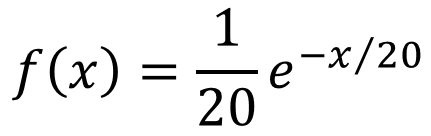
　　通过这个函数我可以求出等待每一分钟的概率值。由于20分钟是一个期望值或均值，因此实际等待的时间可能会比这个短一些，也可能会更长。假设我已经等了10分钟的时间，现在不愿意过多的等待，又不想浪费时间。因此我想知道再继续等待5分钟就可以进去用餐的概率有多少，如果概率较高的话，我就继续等待一会儿，如果概率低的话，我就先去逛逛商场，然后在晚一些回来。假定这个时间是30分钟，那么我想知道这时候可以进去用餐的概率有多少。以上这两种情况的判断用累积概率的计算公式可以获得。

　　将平均等候时间20分钟和我们希望获得的等候时间30分钟代入到累积概率的计算公式中。可以求出等候30分钟以内可以用餐的概率。

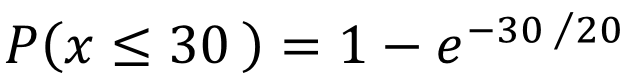
　　分别求出等候15分钟以内可以用餐的累积概率，及等候10分钟以内可以用餐的累积概率，然后将两个概率值相减就可以求出再等候5分钟（10分钟-15分钟）以内可以用餐的概率。

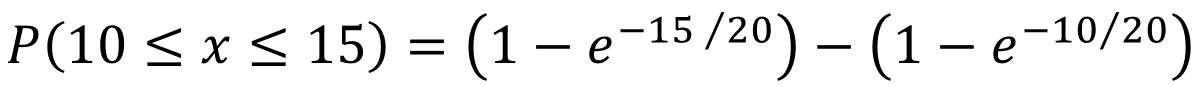
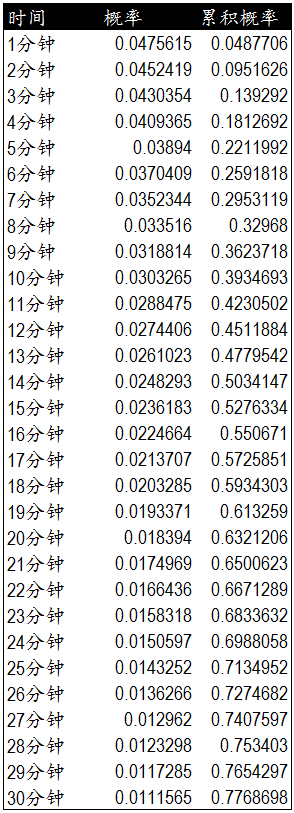
　　以下我们分别计算出在餐厅平均等位时间为20分钟的情况下，等待1-30分钟可以用餐的概率和累积概率。

　　将这些概率值绘制成餐厅等位时间概率密度图可以更直观的说明计算的过程。在下面的概率密度图中，X轴表示等候时间，从1分钟到30分钟。Y轴表示概率密度函数的值。整个图形区域的概率（面积）之和为1。当我们计算等候30分钟以内可以用餐的概率时，就是在计算图形中蓝色区域的面积。而当我们就计算等候1分钟后再继续等候5分钟以内(10分钟-15分钟)可以用餐的概率时就是在计算图形中绿色区域的面积。

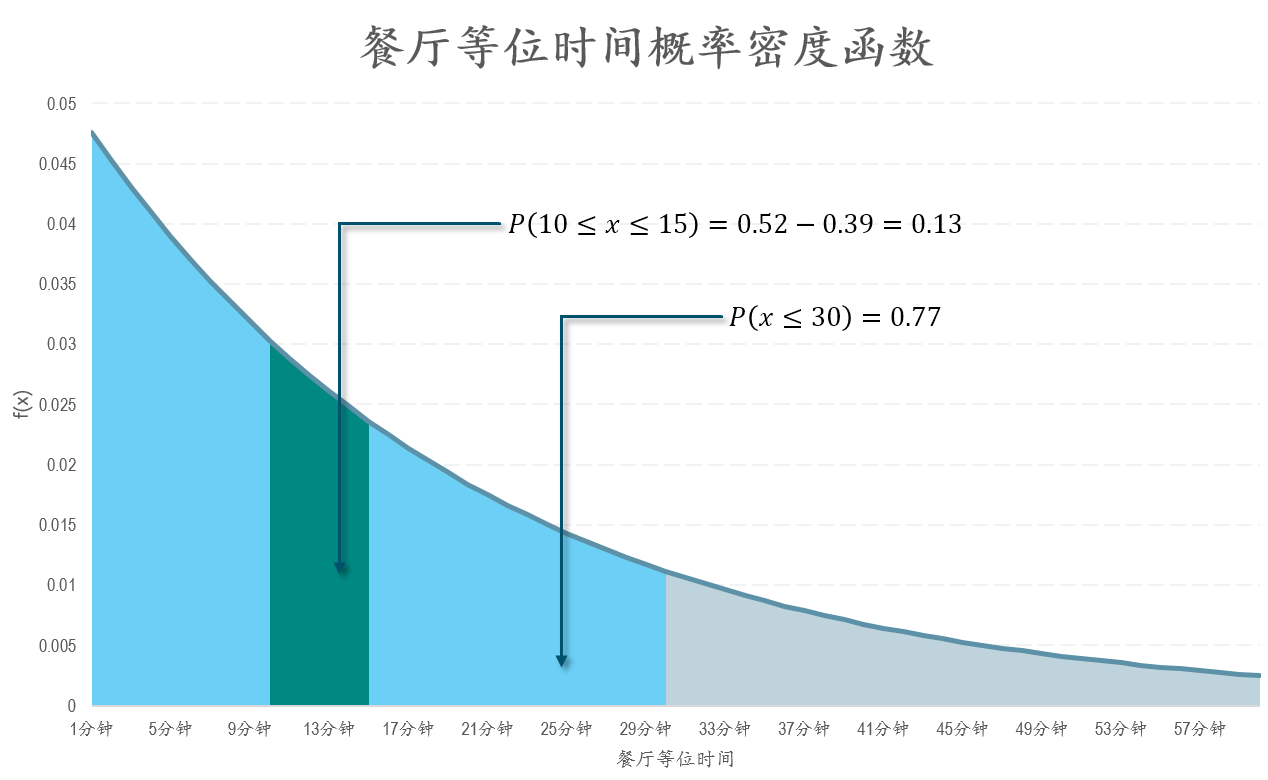
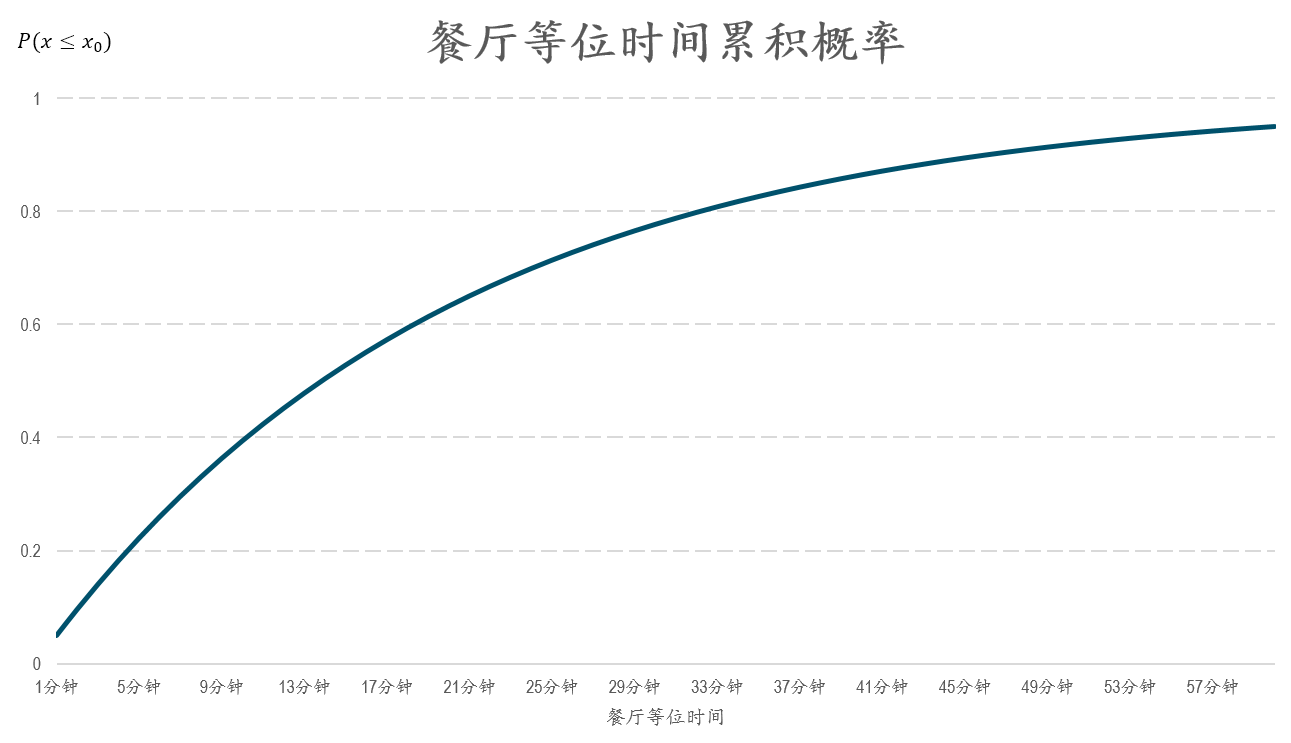
　　通过计算可知再等候5分钟(10分钟-15分钟)可以用餐的概率为0.13（连续等等15分钟的累积概率为0.52），30分钟内回来可以用餐的概率为0.77。因此我可以选择先去逛15分钟，在30分钟时回来。如果你希望精确的获得等待每1分钟用餐概率的变化情况，可以绘制累积概率图，以下是餐厅等位时间的累计概率。X轴表示餐厅等位时间，从1分钟到60分钟。Y周围累积的用餐概率。可以看到用餐的概率随等候时间的增加而增长，最终的累积概率值为1。