当我们谈论正方体时，我们能谈些什么？

　　点击标题下面一行中的蓝字“数学教学研究”，关注本微信公众号。本公众号每周推送两到三篇数学趣文，力争做到深入浅出。

　　美国作家雷蒙德·卡佛有本小说集叫《当我们谈论爱情时我们在谈论什么》。

　　那么我们在谈论正方体时，我们能谈些什么呢？

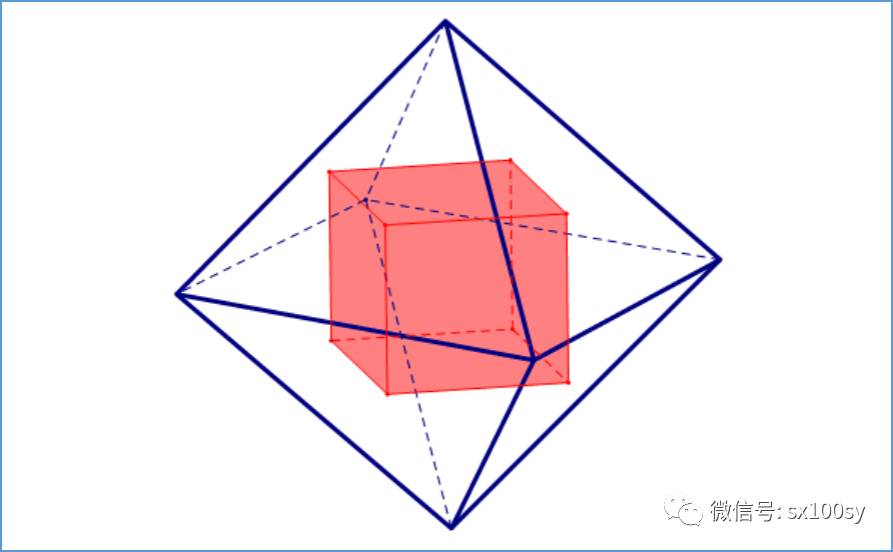
　　一、正方体隐藏于正八面体中

　　以正八面体八个正三角形面中心为顶点的正多面体就是正方体。本期内容尽量把立体图形画得立体感强一些，但仍需要您的想像力。

　　二、正方体隐藏于正十二面体中

　　隐藏在正十二面体中的正方体以正十二面体正五边形界面的对角线为边。每个五边形都有五条对角线，所以，正十二面体内共有五个不同位置的正方体。可以粗略计算一下：正十二面体有12个面，每个面有5条对角线，这样一共有60条对角线。而一个正方体有12条棱，共有5个正方体，所以一共是60条棱。数量上是相等的。您若有时间可以逐个画出，便可看出确实只有五个不同的正方体，它们用到了全部60条对角线，并且一条对角线用且只用一次。下图只画出一个。

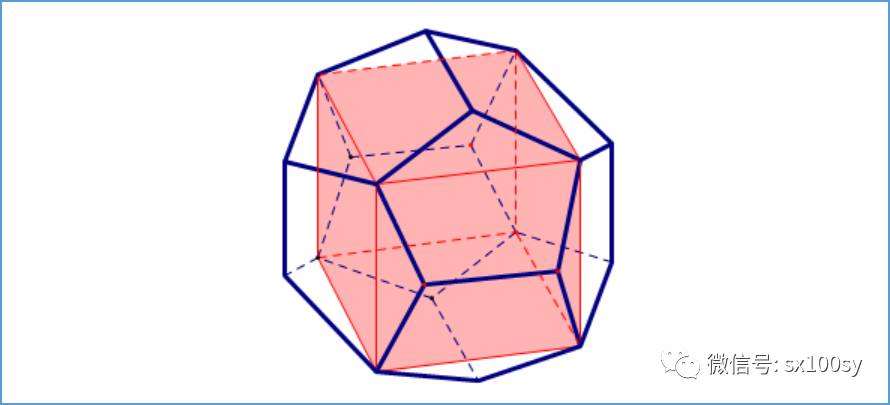
　　可以把正十二面体理解为：在一个正方体的六个正方形界面的外面各扣上一个完全相同的“屋脊“。这6个“屋脊“是确定的，即“屋脊“的四个斜面的倾斜角是确定的，以使得有公共边的两个“屋脊“中，一个“屋脊“的等腰梯形斜面与另一个“屋脊“的等腰三角形斜面合在一起位于同一个平面内，构成正十二面体的一个正五边形界面。如下图示。

　　三、正方体隐藏于菱形十二面体中

　　这里说的菱形十二面体与上面所说的正十二面体是完全不同的。正十二面体是仅有的五种柏拉图正多面体之一，这是完美对称的。而菱形十二面体则没有那么多完美的对称性。菱形十二面体似乎不太好想像，所以，我们用正方体和正四棱锥这些简单的形体来构成它。如下图所示，中间是一个正方体，类似前面构成正十二面体，但这里是在正方体的每个正方形面上各扣上一个正四棱锥，这6个四棱锥的底面是正方形（与正方体的面全等），侧面是全等的等腰三角形。锥的侧面的倾斜角是45度。于是，以正方体的一条棱为公共棱的两个正四棱锥，它们各自的一个侧面在公共棱处合在一起，位于同一个平面内，并构成一个菱形，而原正方体的这个棱消失在这个新产生的菱形中（成为它的一条对角线），请观察下图中绿色菱形。又因为正方体有12条棱，消失一条棱意味着产生一个菱形，所以共产生12个菱形。这就是它被称作菱形十二面体的原因。

　　四、正四面体也与正方体有关

　　看似不可能，但确实有关，还很密切。为什么这么说？我们先画一个正四面体。

　　注意其中的棱AC和BD。它们异面垂直。我们画出它们的公垂线EF，其中E和F分别是AC和BD的中点。如下图。

　　接下来，把这个正四面体绕EF旋转90度。结果如下图所示。观察除E和F以外的那8个点（A、B、C、D、A'、B'、C'、D'）。

　　我们把它们连接起来，注意，原来已经有连线的不考虑。我们把新的连线涂以红色。如下图所示。

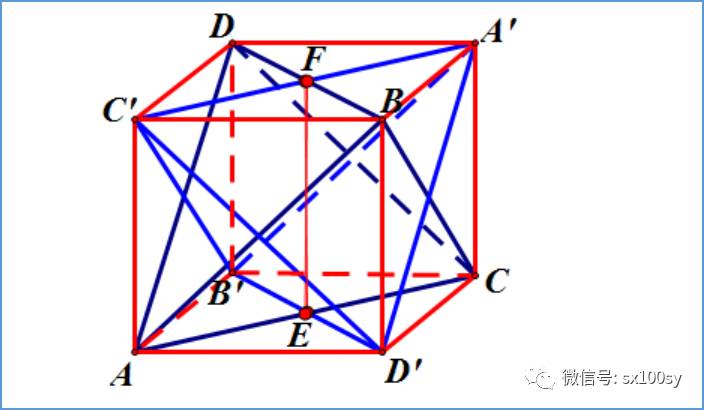
　　这个红色结构就是一个正方体。

　　我们可以把两个正四面体看成是“长”在一起的。如下图所示。

　　再仔细想一想，上图中粉红色和橙黄色两个“长”在一起的正四面体，它们的公共部分是什么？ 对的，是正八面体。这个正八面体的六个顶点是图中红色正方体六个面的中心。

　　结合本文第一条中所说，可以发现：

　　（1）一个正八面体各面中心是一个正方体的顶点。

　　（2）一个正方体各面中心是一个正八面体的顶点。

　　（3）在一个正八面体的各个面上都"粘"上一个正四面体，就得到上图所示长在一起的”连体四面体”（我起的名字，不是标准的叫法，其实它有24个正三角形面）。这个”连体四面体”的8个尖顶是正方体的8个顶点。

　　五、正方体是五种柏拉图正多面体中唯一能够铺满空间的立体

　　我们把无数多个同样大小的正方体面对面、棱对棱、顶点对顶点地放到一起，就可以做到之间不留任何空隙地铺满整个空间（其实正方体太规整了，很容易堆满空间，不一定像魔方那样靠得那么整齐，错位也是可以的，但不能留空隙是必须的）。那么，我们前面介绍的菱形十二面体也是可以做到不留空隙地铺满整个空间。怎么理解呢？

　　我们从平面情形说起，然后空间情形就容易理解了。有四个正方形，如下图左图放置成十字型，中间空出一个正方形大小的区域：

　　我们把这四个正方形比做军队，它们同时以同样的火力向中间区域进攻。那么，它们一定最终各占据一个等腰直角三角形的区域。四个等腰直角三角形正好填满这个正方形（如上图右图所示）。

　　那么拓展到空间情形，则是六方军队同时攻占中间正方体空间区域。同样也是势均力敌，那必然是各抢占六分之一的空间，这六分之一的空间是一个正四棱锥。六个正四棱锥对在一起，正好填满一个正方体空间。

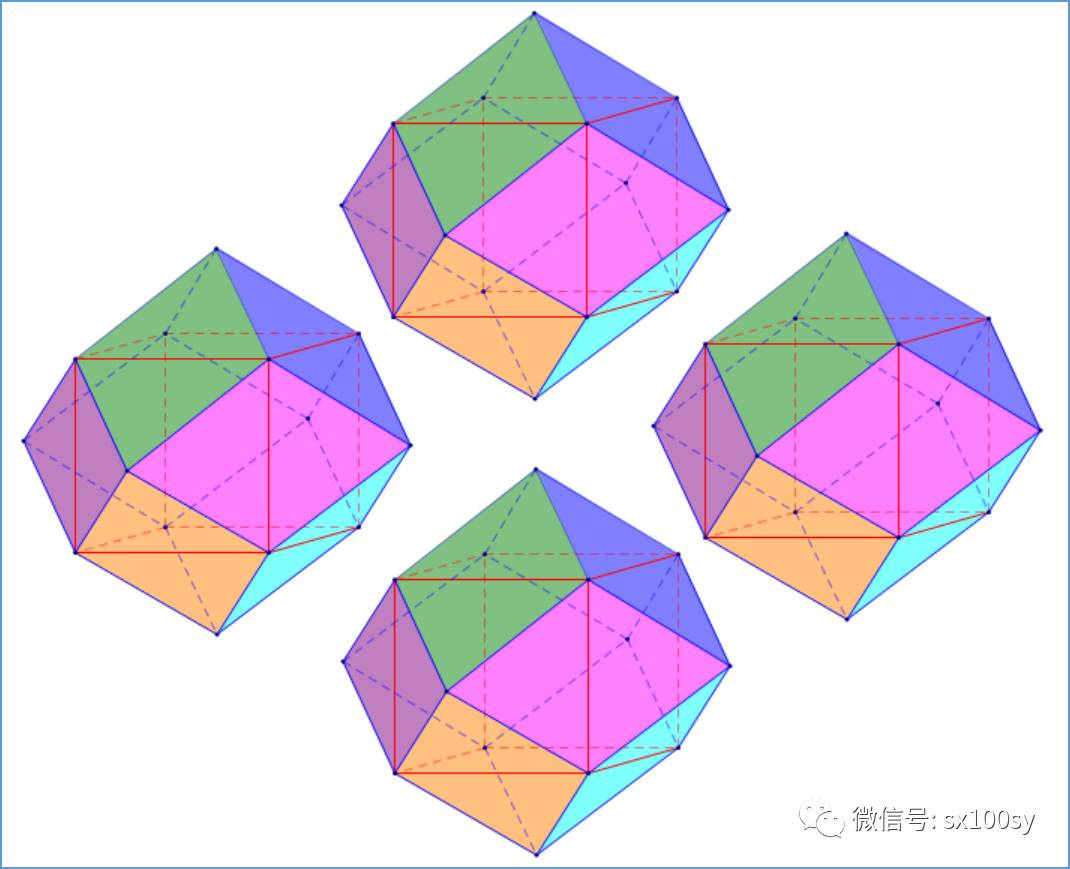
　　上图是4个完全一样的菱形十二面体，一左一右，一上一下。我们准备把它们靠拢在一起，那么，左边立体的右上菱形界面与上边立体的左下菱形界面将对在一起。同理，左边立体的右下菱形界面与下边立体的左上菱形界面将对在一起。右边立体的左上菱形界面与上边立体的右下菱形界面将对在一起。右边立体的左下菱形界面与下边立体的右上菱形界面将对在一起。再调用两个同样的菱形十二面体，一前一后对到中间。很容易看出，这6个菱形十二面体各贡献出一个正四棱锥，6个锥顶对在一起，在中间正好拼出一个正方体。其实，每个菱形十二面体在6个方向上都贡献出一个正四棱锥，从而可以得出一个菱形十二面体的体积是两倍的正方体体积。

　　所以，我们说正方体可以充满空间，这就意味着从正方体变化而来的菱形十二面体可以充满空间。石榴的果实是一个实际例子。