
关注萌萌说
半角模型——由黄浦二模25题说起
事情由来
萌萌上周解析黄浦二模卷的时候,做第25题做起来尤是吃力,特别是解析第三小问时使用了一个方法偏相似和三角比公式的做法,计算强度相当大。

后面萌萌才发现此题其实使用初二所学的半角模型更加简单,便利,所以这里给大家一起来科普下半角模型。
模型概况
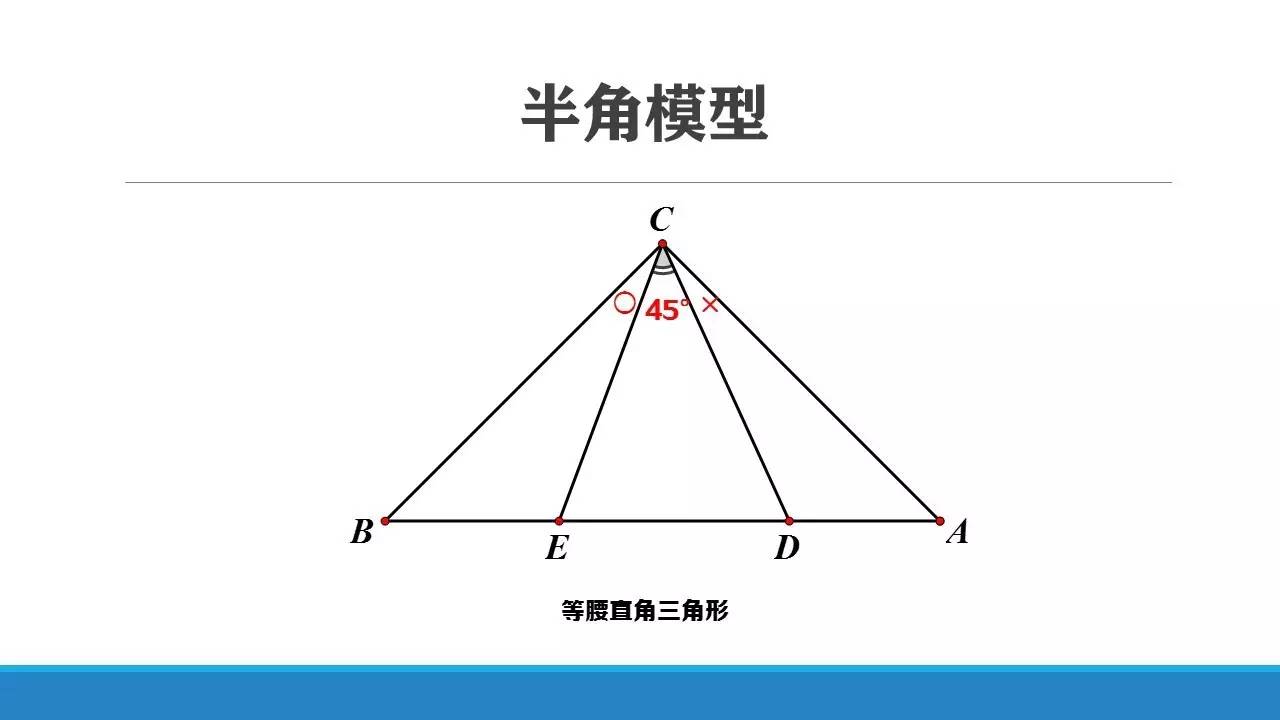
过*等腰△ABC(BC=AC)顶角顶点(C),引两条射线且它们的夹角为C/2;这两条射线与过底角顶点的相关直线交于两点E、D,则BE,ED,AD之间必存在固定关系。这种关系仅与两条相关直线及顶角C相关.
*注:不需要一定是等腰△(需要初三知识)。
模型解法
【1】翻折法

拿黄浦25举例,○+×=45度,将○角与×角进行翻折之后,角的两条边共线(重合)。

左图为等腰直角三角形,角的两条边重合,
右图为直角三角形,角的两条边共线。

通过直角三角形的两锐角互余,如上图(红色部分)可得到垂直关系,通过勾股定理,即可得到25(2)(3)的答案。
【2】旋转法
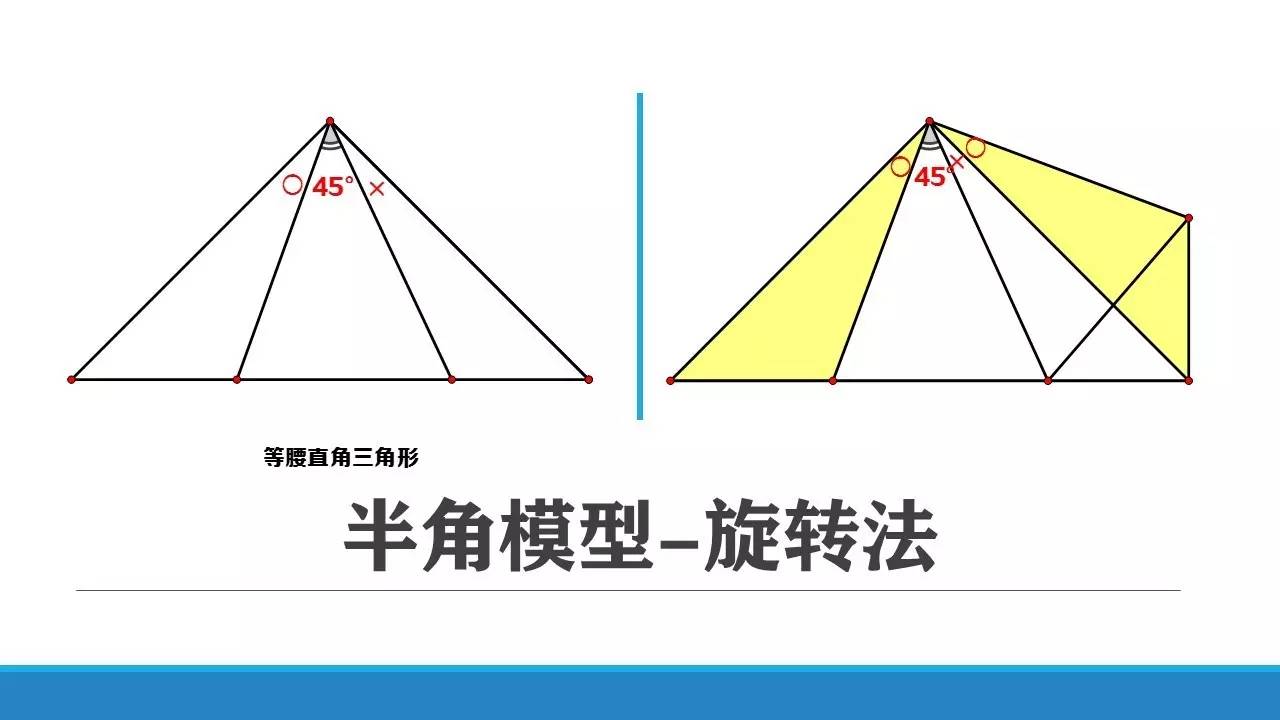
拿黄浦25举例,将黄色三角形旋转90°。

通过○+×=45度,可证明蓝色的两个三角形全等。
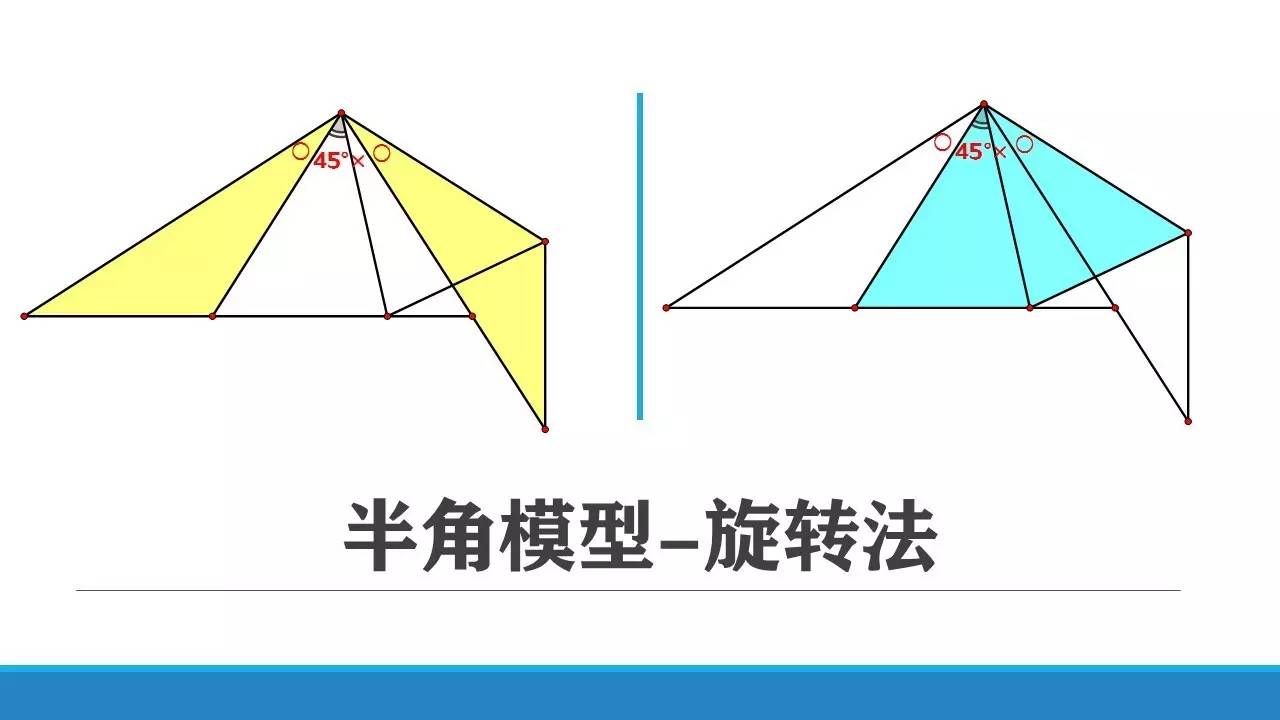
如果三角形不是等腰直角三角形,将黄色三角形旋转90°,同样可证明蓝色的两个三角形全等。
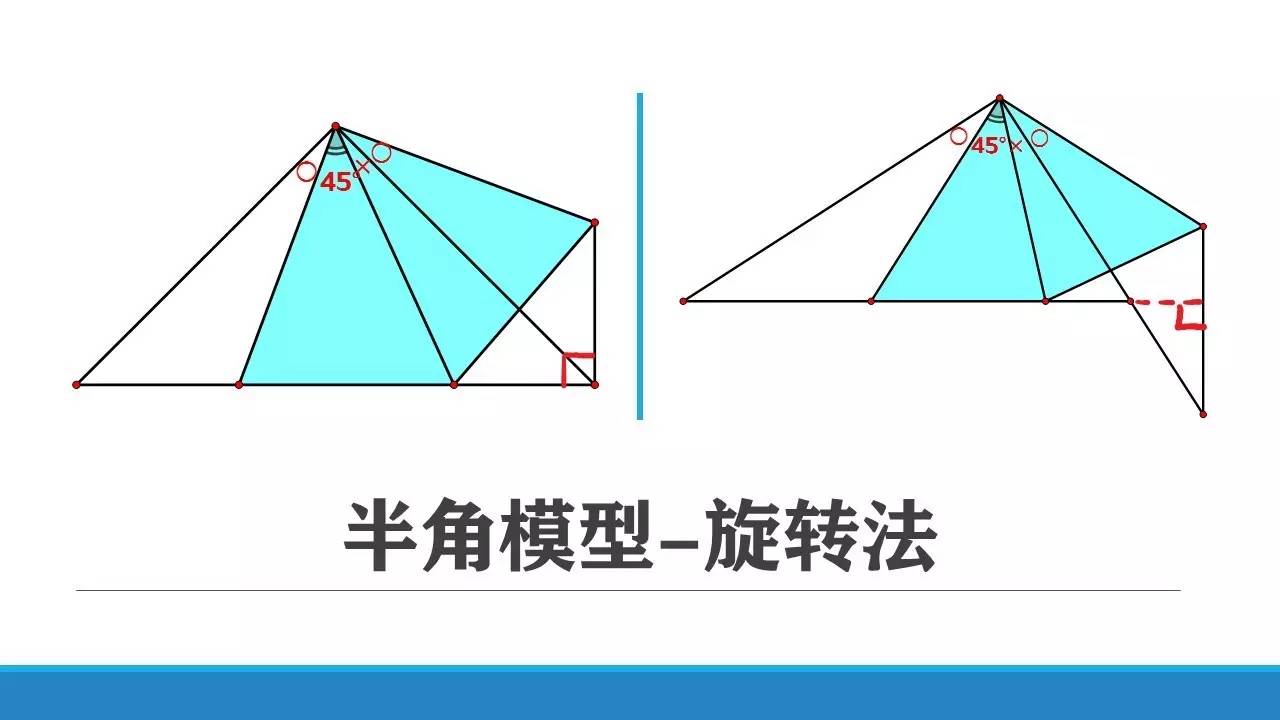
通过直角三角形的两锐角互余,如上图(红色部分)可得到垂直关系,通过勾股定理,即可得到25(2)(3)的答案。
模考原题

纵观上海模考卷,比如2012年浦东二模25,甚至是2014普陀一模25都涉及到半角模型。
例题



结语
半角模型是初二几何教学中非常重要的模型,甚至在初三的试题中也有其一席之地,希望大家要更加全面地复习总结,备战中考!!!
【好文回顾】
 )
)





























我来说两句排行榜