用塞瓦定理
证明几个重要三线共点问题
我们知道,一个三角形的三条中线共点,三条垂线共点,三条内角平分线也共点。其中有的容易看出,有的却不太容易。那么,这里,我要从塞瓦定理出发,来证明这三个共点问题。
先说塞瓦定理和塞瓦定理的逆定理。
塞瓦定理:有一个三角形ABC,点X、Y、Z分别是BC、CA、AB上的点。如果它的三条塞瓦线AX、BY、CZ共点,则有下式成立:
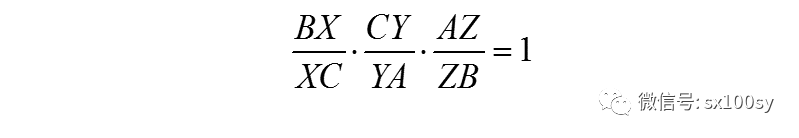
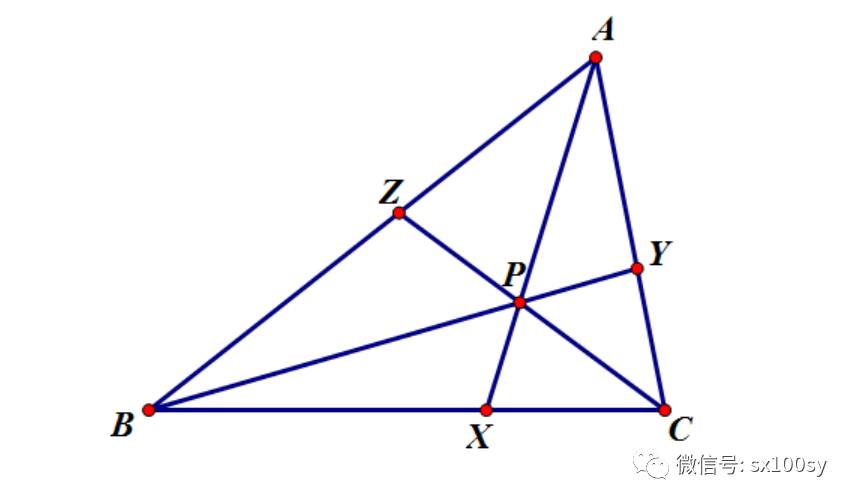
证明:
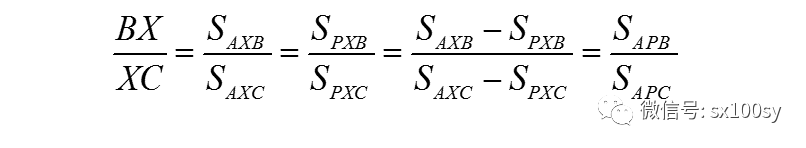
同理
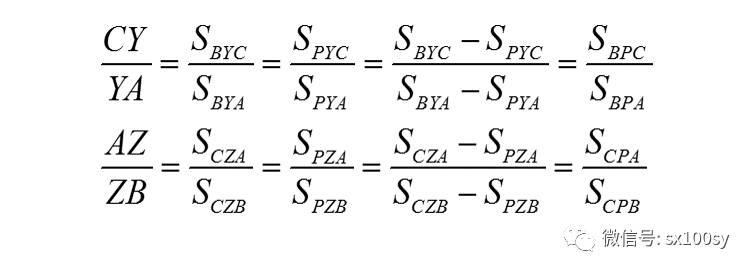
以上三式相乘,得

塞瓦定理的逆定理:有一个三角形ABC,点X、Y、Z分别是BC、CA、AB上的点。如果下式成立
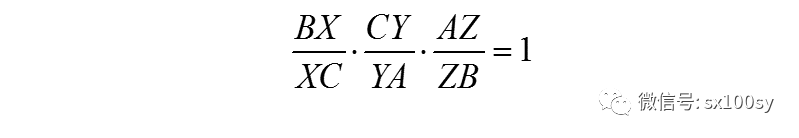
那么它的三条塞瓦线AX、BY、CZ共点。(证明略)
(1)用塞瓦定理的逆定理可以很轻松证明三角形三条中线交于一点。这是因为X、Y、Z分别是三边BC、CA、AB的中点,所以BX=XC,CY=YA,AZ=ZB。所以
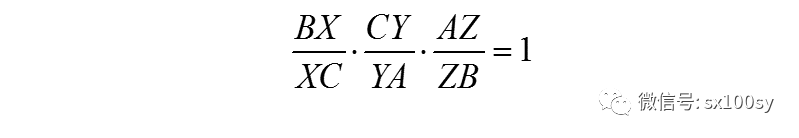
所以三条中线共点,这个点就是重心或中心。
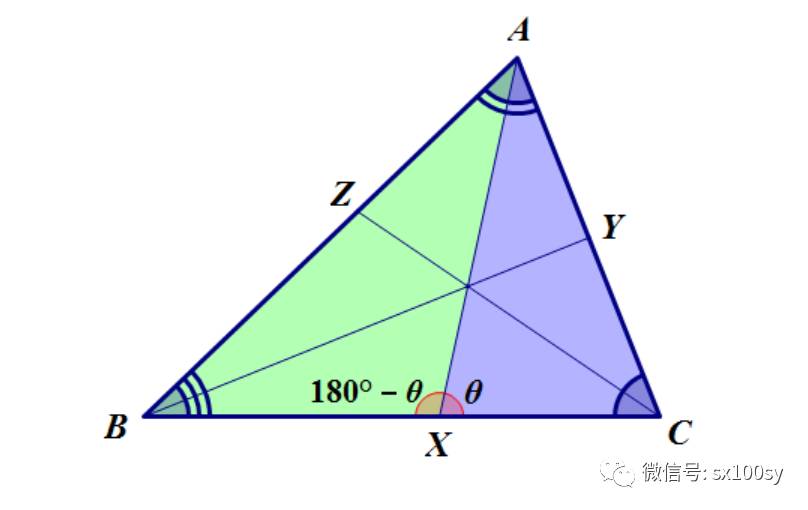
(2)下面用塞瓦定理的逆定理证明三角形三条垂线交于一点。如下图所示,AX、BY、CZ分别为BC、CA、AB边上的垂线。
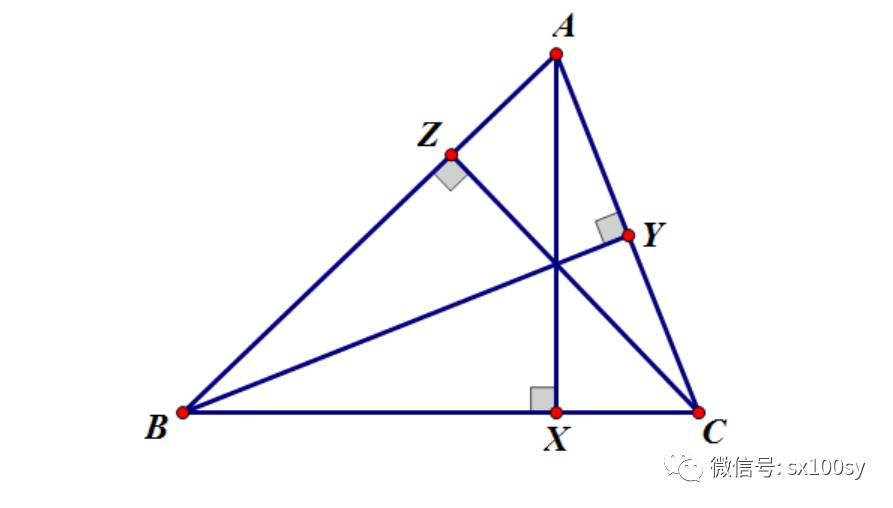
因为

把上面三式相乘,得
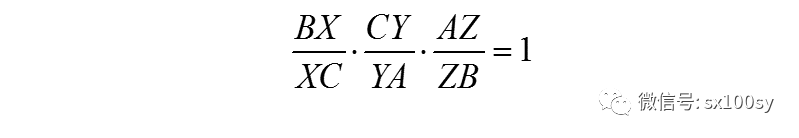
所以,三条垂线交于一点,这个点就是垂心。
(3)下面用塞瓦定理的逆定理证明三角形三条内角平分线交于一点。如下图所示,根据正弦定理,有
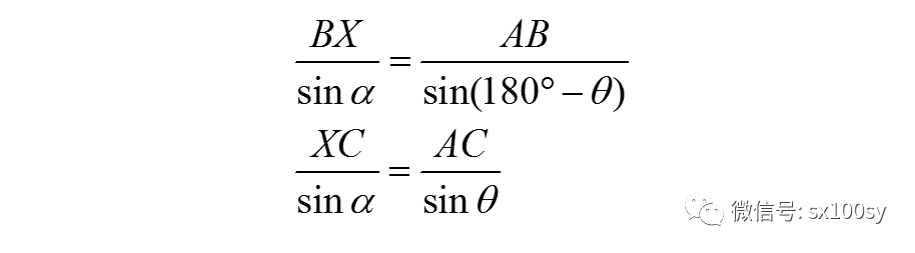
两式相除,得
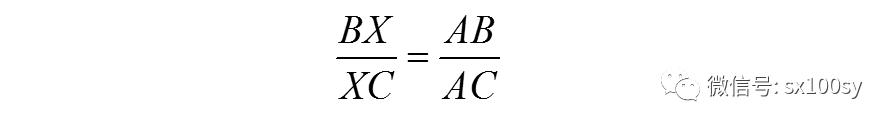
同理可得
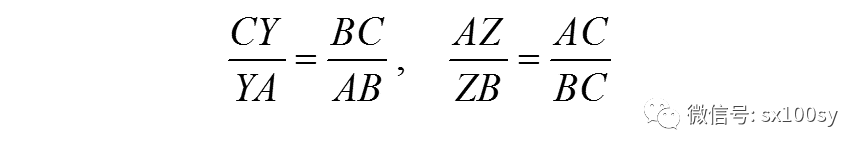
以上三式相乘,得
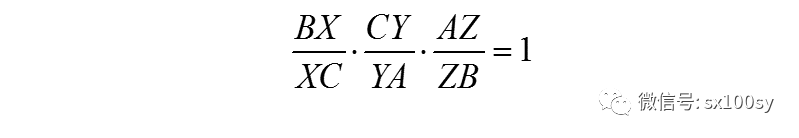
所以,三线共点。其实,这个点就是三角形ABC的内切圆的圆心,即内心。
下一期讲塞瓦定理与梅涅劳斯定理的关系,但大概要到本月15号才能推送了,这是因为本人近四五天要外出,故不能每天推送了。本期还是利用了微信的定时发送功能,但这个功能只能今天设置今天和明天发送,后天及以后不能设定。您可以重读以往的内容,也可以休息一下大脑,待我回来后再交流。

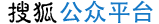
 )
)






























我来说两句排行榜