5.2 供给定律
内容提要:本节根据广义动量定理Fαt=nmV中的力量分析得到供给定律公式,并且进一步推导得到供给弹性。在广义动量定理中,合外力F决定成果nmV,合外力越大,成果越大。在供给定律中,商品的价格P是供给者提供商品的动力,商品的成本C是供给者提供商品的阻力,二者的合力P-C为供给者盈余,这个合力决定供给量QS这个成果。KS为供给者盈余转化率,所以商品的供给量QS=KS(P-C),这个公式为供给定律公式。由供给定律可以推导得到供给弹性公式为

创新要点:
1. 提出了供给定律公式QS=KS(P-C),这是以前经济学所没有的,完善了经济学中供给定律没有公式的缺憾。
2. 给出了供给定律的图形,指出了供给定律与坐标轴的交点,以前的供给曲线和坐标轴是没有交点的。并且给出了价格,成本和盈余转化率变化对供给量的影响。因为有了供给定律公式,每一个量的变化对供给曲线的影响一目了然。
3.给出了供给弹性的推导过程,供给弹性是根据供给定律推导而来。
4. 给出了供给定律的推导过程,指出供给定律的本质是广义动量定理,价格与成本之差的这个合力决定了供给量。
经济学上,供给定律指的是这样一条基本规律,即某种商品的供给量与其价格呈正方向变动。具体而言,对于正常商品来说,在其他条件不变的情况下,商品价格与需求量之间存在着正方向的变动关系,即一种商品的价格上升时,这种商品的供给量就会增加,相反,价格下降时供给量减少,这就是供给定律。因此,供给定律反映的是商品本身价格和商品供给量之间的关系。供给定律与需求定律是类同的。
5.2.1 供给定律公式商品的价格与供给量正相关,价格越高,供给量越多;商品的成本与供给量负相关,成本越高,供给量越少。生产者盈余=商品的价格-商品成本,所以生产者盈余与供给量正相关。设商品的价格为P(Price),生产者盈余为SS(Surplus),供给量为QS(Quantity),生产者盈余转化为购买量的函数为KS,则
QS=KS (P-C)

图5-19 供给曲线
在横坐标为供给量QS,纵坐标为价格P的坐标系中,SS为供给曲线。价格P为C时的供给量为0。现实中,不同的供给量所对应的成本C是不同的(如图5-19所示)。
a)成本C变化导致供给曲线的移动
原供给曲线函数为QS=KS(P-C),供给曲线S1S1与价格P坐标轴相交于C点。税收等原因导致成本从C上升到C+T,供给函数变为QS=KS(P-(C+T)),供给曲线S2S2与价格P坐标轴相交于C+T点,供给曲线上移T距离。在相同的价格PA下,供给量从QA下降到QB(如图5-20所示)。

图5-20 供给曲线的平移
b)价格P变化导致供给量变化
供给曲线函数为QS=KS(P-C),供给曲线SS与价格P坐标轴相交于C点。竞争等原因导致价格从PA下降到PB,供给量沿供给曲线SS从QA下降到QB(如图5-21所示)。

图5-21 沿供给曲线变动
c)政策和环境等原因导致KS的变化
供给曲线函数为QS=KS1(P-C),供给曲线S1S1与价格P坐标轴相交于C点。政府的政策鼓励等原因导致盈余转化率从KS1上升到KS2,供给曲线从S1S1变为S3S3。此处注意纵坐标是自变量,所以S3S3在S1S1下。在相同的价格PA和成本C的情况下,供给量从QA上升到QC。勤劳民族的盈余转化率要比安逸的民族的盈余转化率大,灾难后的盈余转化率比平时要大(如图5-22所示)。

图5-22 供给曲线斜率的变化
5.2.2 供给定律与供给弹性供给弹性是供给定律的一个数学推论,是供给定律的微分形式。供给弹性等于盈余转化率与基础值的乘积。即

。
为了方便起见,在没有与需求定律混淆的地方,省略部分下脚标。即供给弹性为

供给的价格弹性(price elasticity of supply),衡量的是:当一种物品的价格发生变动时,该物品供给量相应变动的大小。供给弹性的准确定义是供给量变动的百分比除以价格变动的百分比。即

推导过程:
需求定律公式为Q=KS(P-C),通过数学对价格P求微分,KS也可以看做常数,对应不同的消费者盈余(P-C),KS为不同的常数。所以有:

两边同时除以ΔP,并且乘以P/Q,得

对比供给弹性公式,得到:

其中C(ΔP)为价格变化对成本的影响,是成本关于价格的函数。
由于对于大多数商品,成本不随价格改变而改变,在这种情况下,从C(ΔP)等于0,所以得到

由于P/Q为基础值,是常数,所以供给弹性等于盈余转化率与基础值的乘积。KS等于ΔQ/ΔP,KS为正值。
5.2.3 广义动量定理与供给定律公式供给定律公式QS=KS(P-C)是广义动量定理Fαt=nmV的简化。
在供给定律公式Q=KS(P-C),价格P是动力,成本C是阻力,而P-C为合外力F。力量的终极来源有暴力,财富和知识,而供给定律公式中的的主要力量是财富,是财富这个合力产生成果。数量Q对应广义动量定理中的n。将供给定律公式完整化,得到完整供给定律公式(P-C)KSt=QmV。P-C为合力F,KS对应α,Q对应数量n,m表示产品的品类,质量等。在完整供给定律公式中,速度V表示某一产品m的产出速度。完整供给定律公式的表示力量P-C在时间t上的积累效应。合力P-C越大,时间t越长,成果QmV越大。针对某一产品m,m不变。在供给需求定律公式中,增加价格P,减少成本C,增加力量的方向准确性即盈余转化率,增加力量打击作用点的准确性(TOC制约理论就是增加系统打击点的准确性来增加成果),增加时间t都可以增加成果QmV。完整供给定律增加了时间t因素,使经济学具备了动态因素。广义经济学的本质也是广义动量定理。
5.2.4 成本的碗型曲线在战争中,克劳塞维茨说有胜利的顶点;在管理学上有利润曲线和高德拉特所说的浴缸曲线(如图5-23所示);在经济学上有拉弗曲线和成本曲线;这些曲线都是碗型的,上升和下降沿可能不是对称的。

图5-23 碗型曲线
克劳塞维茨在《战争论》中写道:“胜利者不是在每次战争中都能彻底打垮敌人的。胜利常常而且在大多数情况下都有一个顶点。这是大量经验所充分证明了的。于是就发生了如下的情况:大多数统帅宁愿在远离目标的地方停下来,而不愿离目标太近;而有些具有出色的勇敢和高度的进取精神的统帅往往又超过了目标,因而达不到目的。所以只有那些能用少量的手段创建大事业的人才能顺利地达到目的。”
关于成本曲线,肯定会存在一个成本的最低点。刚开始生产某种产品,肯定不能立刻达到成本的最低点,随着管理进步,技能熟练和规模效应等原因,成本在下降,最终达到成本的最低点。此时再增加人力,资本或材料等的投入,边际的利益在下降,成本会增加(如图5-24所示)。

图5-24 成本碗型曲线
在固定成本C下,供给曲线为S1S1,与纵轴的交点为C。当成本曲线为碗型曲线C1C1时,供给曲线变为S2S2。可以设置成本函数为一个开口向上的抛物线C=a(Q-b)2来表示碗型曲线。供给函数为QS=KS(P-C),由于纵轴为价格,横轴为供给量,为了绘图方便,需要将供给函数进行变换,得到P=QS/KS+C,带入碗型成本曲线,得到新的供给函数为P=QS/KS+a(Q-b)2,绘图得到供给函数图形为S2S2(如图5-25所示)。

图5-25 成本碗型曲线对供给曲线的影响
成本函数有许多形状,碗型成本曲线只是其中的典型形状之一,对于不同的成本曲线,只要根据供给函数QS=KS(P-C),将成本C替换成对应的成本函数即可。
摘自《可以量化的经济学》
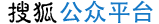
 )
)






























我来说两句排行榜