群论简史及其在物理和化学中的应用

　　The universe is an enormous direct product of representations of symmetry groups.

　　—Steven Weinberg

　　群是抽象代数里面很重要的概念，它是描述对称性的数学语言。

　　Late 1700s- Joseph-Louis Lagrange (1736-1813) 利用置换的概念，理解了三次和四次方程为什么有解。（Paolo Ruffini利用同样的思想证明了一般的五次或以上方程没有根式解）

　　Early 1800s-Évariste Galois (killed in a duel in 1832 at age 20), and Niels

　　Abel (died in 1829 at age 26 of TB) 阐述了代数方程的可解性和置换群的联系，真正利用群的概念解决了这个难题。

　　第一个正式的群的概念由Cayley于1854提出。Cayley, Hamilton, and Sylvester 引进了矩阵的表达。1890年Fedorov发展了各种对称性操作的数学方法，证明了晶体有且仅有230种空间群，次年Schönflies也独立的证明了这个结果。1920年群论开始应用于物理、化学等领域。里面还有很多著名数学家和物理学家的贡献，不一一而举。

　　群论在物理和化学中究竟有啥用？

　　It is often hard or even impossible toobtain a solution to the Schrodinger equation-however, a large part ofqualitative results can be obtained by group theory. Almost all the rules of spectroscopy follow from the symmetry of a problem. -Eugene Wigner (1963 Nobel Prize in Physics)

　　1. 群论在量子力学中的应用

　　举两个很优雅例子：

　　a. 能级简并度的确定

　　Each eigenvalue of a Hamiltonian there corresponds a unique irreducible representation of the group of that Hamiltonian. The degeneracy of an eigenvalue is the dimensionality of this irreducible representation. Thus, the dimensionalities of the irreducible representations of a group are the possible degeneracies of Hamiltonians with that symmetry group.

　　b. 布洛赫定理

　　固体物理中最重要的结论之一，完全可以由群论得出，其证明亦简单。

　　定义一个平移操作

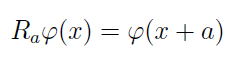
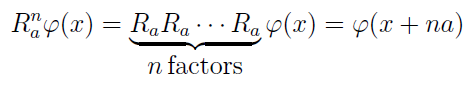
　　可知Hamiltonian是一个N阶的阿贝尔循环群。

　　Character table如下：

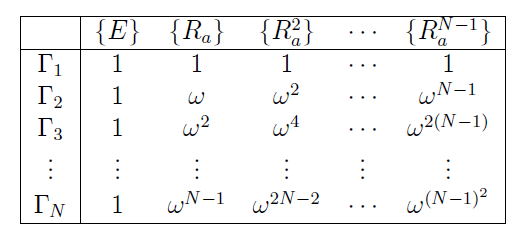
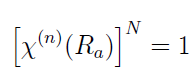
　　便可证明

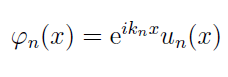
　　更多信息参考：

　　Tinkham, Group Theory and Quantum Mechanics(1964)

　　2. 选择定则（Selection Rules）

　　3.Molecular Vibrations, Infrared, and Raman Activity.

　　4. 能带理论，k dot p model

　　5.

　　未完待续，长期更新。。。

　　------------------------------

　　Ref:

　　"Group Theory: Applications to the Physics of Condensed Matter" by M. S. Dresselhaus

　　“Chemical Applications of Group Theory” by F. Albert Cotton

　　“Molecular Symmetry and Group Theory,” by Carter

　　"Group Theory and Quantum Mechanics" by Tinkham

　　Author(s),Title

　　Ballhausen, Introduction to Ligand Field Theory

　　Ballhausen, Q. M. and Chemical Bonding in Inorganic Complexes

　　Bishop, Group Theory and Chemistry

　　Burdett, Molecular Shapes

　　Albright, Burdett, Whangbo, Orbital Interactions in Chemistry, 2nd Edition

　　Burns & Glazer, Space Groups for Solid State Scientists

　　Butler, Point Group Symmetry Applications

　　Figgis, Introduction to Ligand Fields

　　Flurry, Symmetry Groups

　　Franzen, Physical Chemistry of Solids, Basic Principles …

　　Hanna, Quantum Mechanics in Chemistry

　　Hoffmann, Solids and Surfaces, A Chemist’s View…

　　Heine, Group Theory in Quantum Mechanics

　　Kettle, Symmetry and Structure

　　Lax, Symmetry Principles in Solid State and Molecular Physics

　　McQuarrie & Simon, Physical Chemistry

　　Molloy, Group Theory for Chemists

　　Murrell, Kettle & Tedder, The Chemical Bond

　　Pearson, Symmetry Rules for Chemical Reactions

　　Walton, Beginning Group Theory for Chemistry