毕达哥拉斯学派 与 神奇的三角形数，正方形数 ......

　　毕达哥拉斯（Pythagoras）学派对形数已有所研究，包括三角形数，正方形数，五边形数，等等。并且似乎也知道两个连续的三角形数是一个正方形数。但他们可能没能给出一般的证明。

　　先介绍最基本的三角形数和正方形数，再来研究五边形数及任意k边形数。

（一） 三角形数

三角形数构成一个数列。第n个三角形数是：

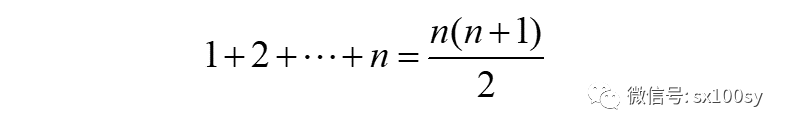
（二） 正方形数

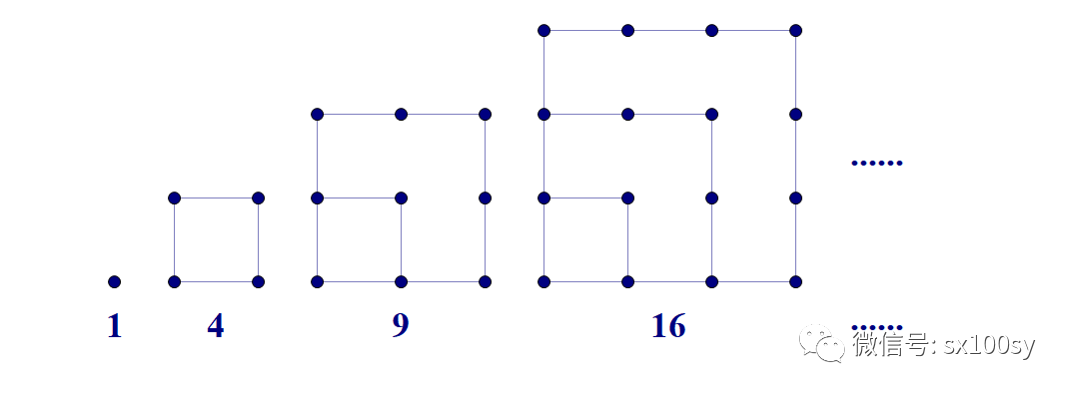
正方形数构成一个数列。第n个正方形数是：

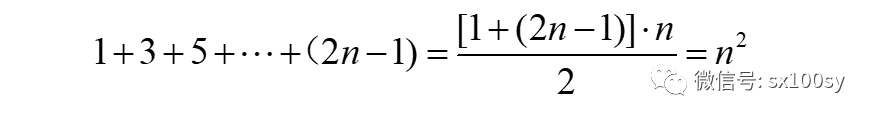
（三） 五边形数

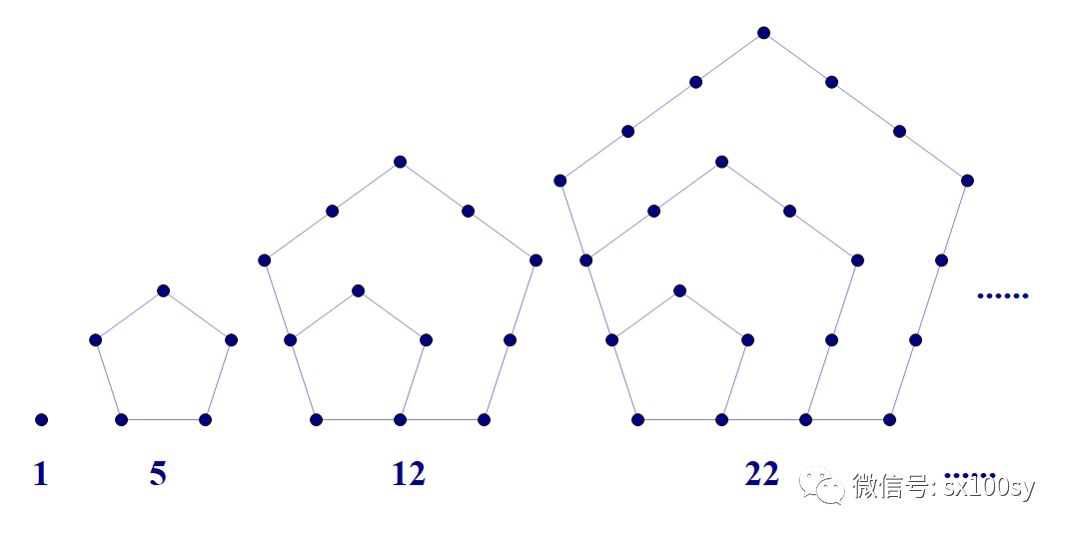
三角形数和正方形数的规律很容易看出来，通项也就很容易写出来。但五边形数怎么求？五边形数的通项公式是什么？先看一下下图：

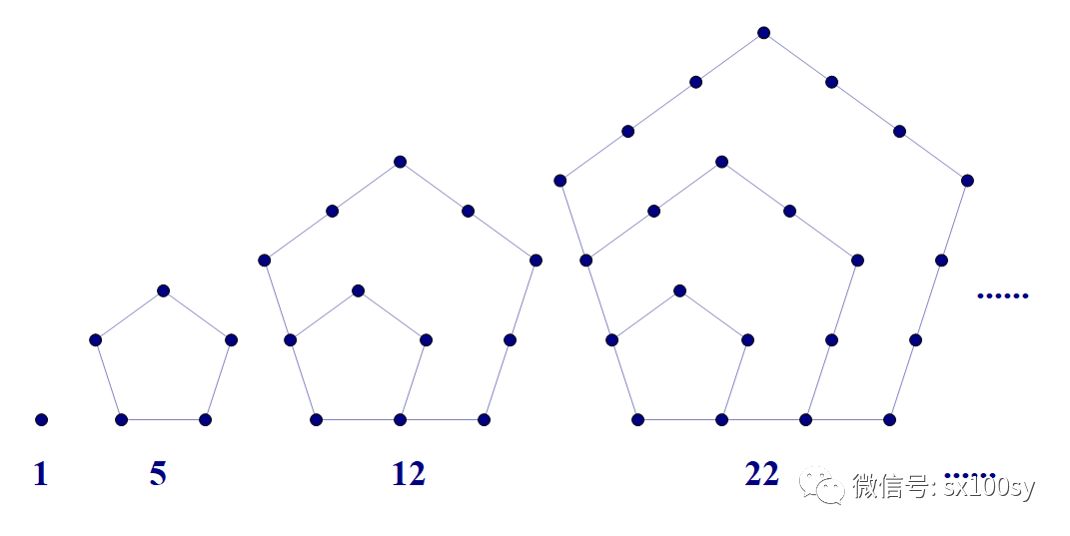
　　您先仔细观察一下。 是不是不太容易找到规律？好的，暂时把这个问题放一放。先说一说简单一些的情况。我们在开始时说过，毕达哥拉斯学派知道两个连续的三角形数是一个正方形数。但为什么？请看下图，我们用了一条斜线（图中红线）把正方形数分成了两部分，这样是不是就很容易看出一个正方形数是由两个连续的三角形数相加而得：左上方为第(n-1)个三角形数，右下方是第n个三角形数，结果是第n个正方形数。

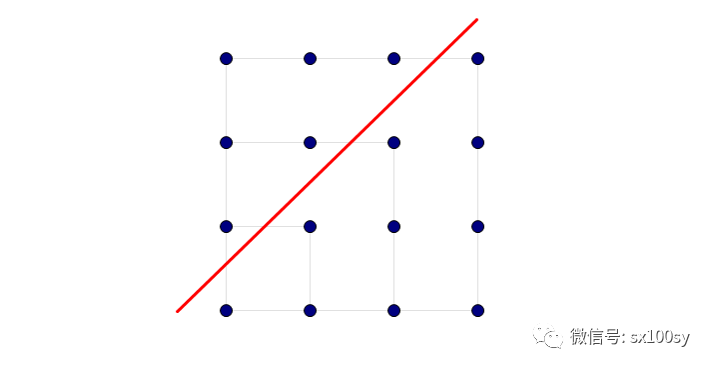
　　我们还可以从通项公式加以验证：

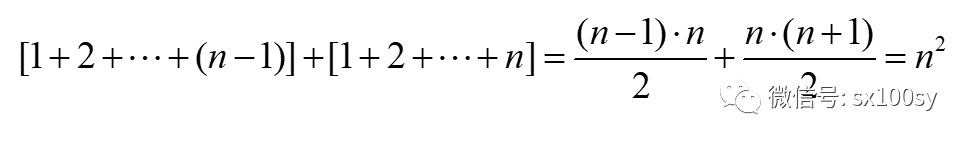
　　把形数重新划分成两部分之后，每部分都化成较简单的形数，这是一种很不错的办法。毕达哥拉斯学派知道把正方形数划分成两个连续的三角形数相加，但他们没有再向前迈进。后来的Nichomachus发展了毕氏学派的研究，他应该是类似地把五边形数也做了类似上面的直线划分，结果，规律显现出来了，如下图所示：

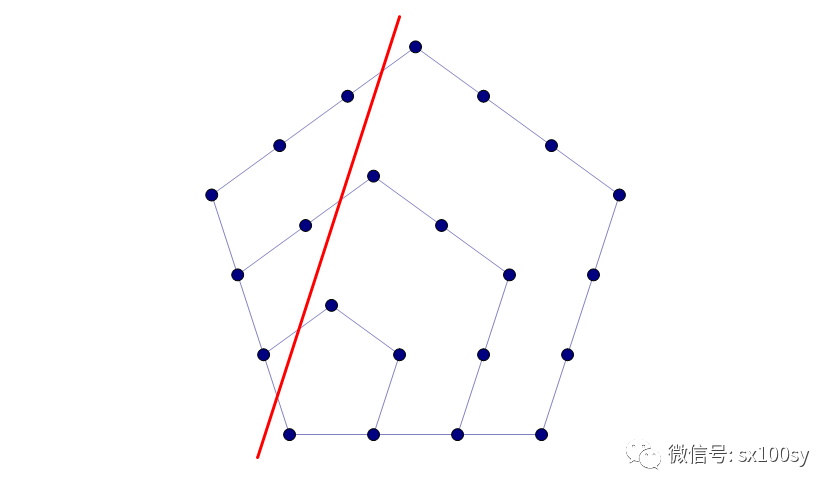
　　您看出来没有，上图中左侧依然是第(n-1)个三角形数，而右侧正好是第n个正方形数。那好的，我们刚才暂时放下没有解决的五边形数的通项公式，现在可以通过上面的划分得到了：

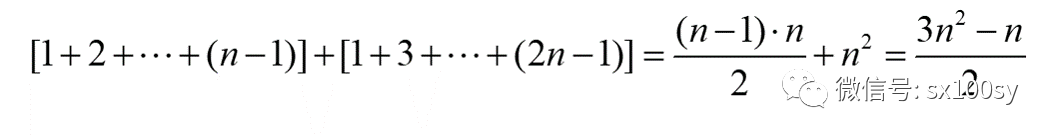
　　再把上面那个五边形数的图形放在这里，你可以用上面的公式验证一下，已画出来的前4个五边形数分别是1，5，12，22都是对的。图中没有画出来的第5个五边形数及之后的五边形数都可以从上面的公式轻松求出。

（四） k 边形数（或叫 k 角形数）

　　下面我们再看一下六边形数，然后，我们就可以最终找到n边形数的计算方法了。

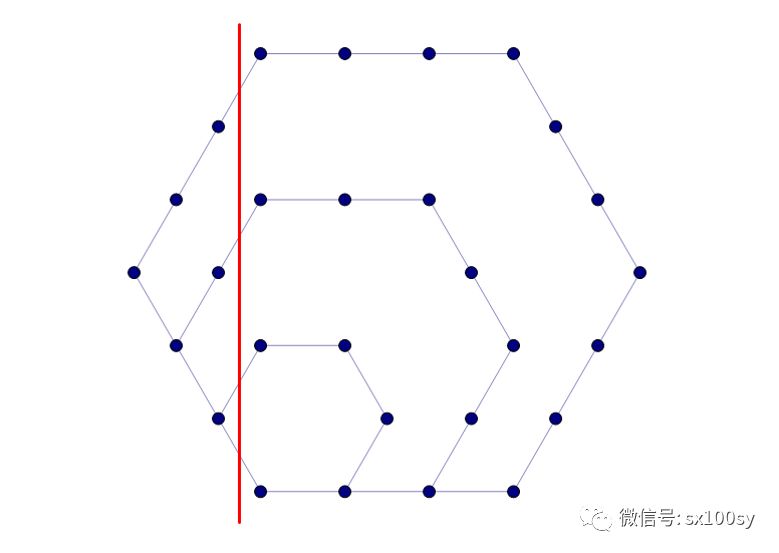
　　六边形数的通项公式可以通过第(n-1)个三角形数加上第n个五边形数得到：

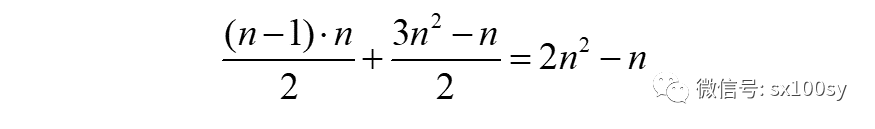
　　为了统一说法，我们下面把k边形数叫做k角形数。那么，我们最终可以得到正k角形数通项公式（项数n的表达式）的计算方法为：第(n-1)个三角形数加上第n个(k-1)角形数。

　　但上面这个算法还是需要一步步地来算，而我们希望得到一个一步到位的统一的公式。也有办法。这个办法是我自己想出来的，没有见到有书上提及。当然不是什么了不起的方法，它是上面方法自然而然的结果。

　　我先给出下面这张划分图，你能读懂它吗？从k角形数划去一个三角形数，然后继续这样做下去，就可以划分出(k-2)个三角形数，它们全都是第(n-1)个三角形数，都可以用n(n-1)/2表示。当然，最后还要加上一排n个点子（图中最下面一排点子）。于是，k角形数的计算公式就是：

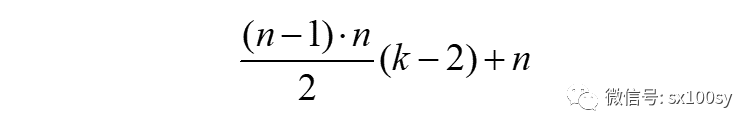
上式中的k取不同值就对应于我们之前所得到的具体的形数通项公式，甚至可以得到任意k角形数的通项公式。取k=3，4，5，6，7时的通项公式分别为：

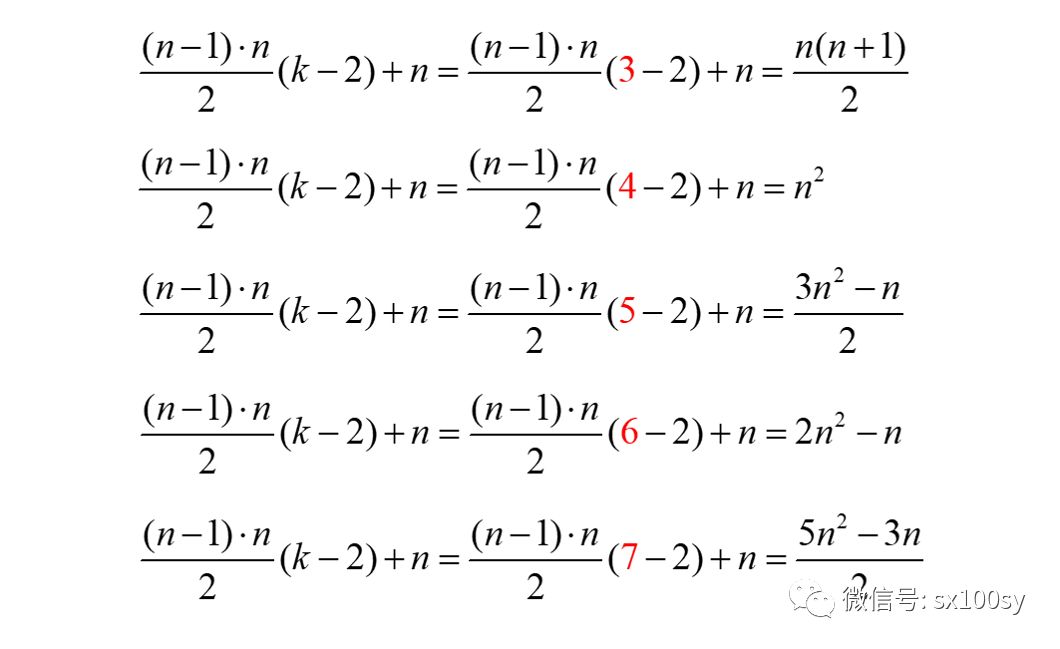
　　前面说到的Nichomachus生活在公元100年左右，他的最大成就是把算术和代数进行独立研究，而不依赖于几何。他的著作《算术入门》是一部完全脱离了几何讲法的算术书。重要性类似于欧几里得的《原本》对于几何的重要性。