
▲点击图片了解“科学三分钟”大赛详情
编者按:
7月21日,多位华人科学家领衔的团队,在当天出版的《科学》杂志上发表论文,报告首次发现了被称为“天使粒子”的马约拉纳费米子的存在证据,引发了公众的极大关注。
马约拉纳费米子的性质十分特殊,是一类反粒子就是其本身的费米子。此次成果发布后,多位物理学家在媒体报道中纷纷发表评论,但说法不一。这次实验是发现了80年前意大利理论物理学家马约拉纳预言并以其名字命名的马约拉纳费米子,还是马约拉纳准费米子?它是高能物理概念中的基本粒子,还是凝聚态物理中的准粒子?相关报道引发了科学家们的认真讨论。
8月4日,《知识分子》编辑部收到论文作者之一、斯坦福大学教授张首晟的来稿,回应相关讨论。与此同时,我们也邀请到论文作者之一、加利福尼亚大学洛杉矶分校教授王康隆,以及麻省理工学院教授文小刚、中国科学院物理研究所研究员戴希就此发表评论。其中王康隆教授对张首晟教授文章中关于该项实验工作实际贡献的叙述提出异议。我们了解到还有其他物理学家在科学上有不同意见,欢迎他们参与讨论。希望此次科学、严谨的学术讨论,对公众和科学界同行理解基本的物理问题和这项工作本身有所帮助。
粒子—准粒子的相对性原理:张首晟就手性马约拉纳费米子的发现答网友问

► 斯坦福大学教授、清华大学教授张首晟。本人供图。
手性马约拉纳费米子的发现(Science357, 294 (2017))引起了广泛的公众兴趣,同时也引出了一些科学问题。理论预言与科学实验使得科学进步; 同样, 科学讨论与客观辩论也能使真理越辩越明。因此,我回答一些科学问题。
粒子—准粒子的相对性原理:爱因斯坦的狭义相对论表明时间不是绝对的;两个观察者观察两个事件之间的时间差取决于他们之间的相对速度。类似地,粒子与准粒子的概念也不是绝对的,而是取决于观察者的能量或长度尺度。以标准模型的能量尺度Es= 10 GeV = 1010 eV出发来测量,凝聚态物理的基本激发,如声子,石墨烯中的狄拉克费米子,拓扑表面状态,与最近发现的手性马约拉纳费米子确实表现为准粒子,因为它们出现在更低的能量尺度Ec= 1 meV = 10-3 eV。这些准粒子由有效的波动方程来描述,该方程的形式与标准模型中的波形方程完全相同。然而,普遍认为,标准模型本身不是终极理论。例如,超弦理论试图在Ep= 1019 GeV的普朗克能标和Lp =10-35 m的长度尺度下来统一量子力学和引力,超弦是基本的实体,而标准模型中的“基本粒子”表现为弦的振动模式。因此,电子和夸克在超弦理论中表现为准粒子,其方式与原子晶格振动的准粒子相似。

► 一维原子晶格中的声子示意图。晶格的长波振动模式(虚线所示)对应于固体中的准粒子, 称为声子。以原子作为基本粒子的观点出发,声子看来是准粒子。

► 超弦理论将基本粒子解释为普朗克尺度下弦的不同振动模式,振动模式的波长反比于”基本粒子”的质量。图中从上到下依次为真空态(不振动),轻粒子如电子(长波振动),以及重粒子(短波振动)的示意图。以超弦作为基本实体的观点出发, 标准模型里的”基本粒子”看来也是准粒子。
我把这基本原理称之为粒子—准粒子相对性原理。粒子与准粒子的概念不是绝对的,而是取决于观察者的相对能量和长度尺度。爱因斯坦的狭义相对论在数学上可以通过洛伦兹变换来精确地表达,同样, 粒子—准粒子相对性原理在数学上也可以通过重整化群来描述。从较高能量和较短长度尺度定义的“粒子”理论出发,可以系统地用积分法除掉高能量和短长度的自由度,并获得在较低能量尺度定义的“准粒子”的有效理论。以这种方式,准粒子的波动方程可以从粒子的波动方程得出,它们往往拥有不同的形式。例如,相对论性狄拉克方程描述静止质量为E = 1 MeV = 106 eV的的电子,但电子在1 eV原子能量尺度上可以被非相对论薛定谔方程描述。但是在1 meV = 10-3eV的能量级上,拓扑绝缘体的表面状态再次由相对论性的狄拉克方程描述。我称这从MeV到meV的狄拉克方程的层展现象(emergent phenomenon),它是自然界美最深刻的表现之一。通常认为,相对论性狄拉克方程比非相对论的薛定谔方程更为基本。因此,从相对论性的狄拉克方程推导出非相对论的薛定谔方程并不奇怪。然而,从描述固体中电子的非相对论薛定谔方程出发,推导出拓扑表面状态的相对论性狄拉克方程是相当令人惊讶的。这是层展概念的最佳说明:有时准粒子可能比粒子本身更有趣。
爱因斯坦的相对性原理是反直觉的,因为我们的日常生活的速度通常远小于光速。 同样,粒子—准粒子的相对性原理也是反直觉的,因为我们习惯于从我们自身的能量尺度来观察事物,不容易达到普朗克能量尺度。 但是我们可以用爱因斯坦的假想实验(Gedanken experiment)方法,让我们的想象力把我们带到普朗克能标。 从那里看,标准模型的“基本粒子”和凝聚态的“准粒子”都是“准粒子”。 凝聚态物理(eV)和粒子物理(GeV)的能量尺度差异为109eV,比普朗克能标Ep= 1019 GeV小十个数量级(10-10)。此时此刻,普朗克能量的观察者只会庆祝人类首次发现了马约拉纳费米子,而不会因为0.00000001%的能量差而争论说这次发现的是粒子还是准粒子。
因此,粒子与准粒子之间没有本质的区别,概念是相对的,正如时间的概念是相对的一样。 粒子与准粒子都在时空传播,满足波动方程。 粒子类型应按照它所满足的数学波动方程来分类。 我们发现的是自然界中第一个满足马约拉纳波动方程的马约拉纳粒子,而粒子与准粒子的区别是不必要的。
传播的马约拉纳粒子和量子马约拉纳束缚态之间的差异:在1937年,Ettore Majorana写下了相对论性的马约拉纳波动方程,用来描述粒子是其自身反粒子的费米子。 马约拉纳的波动方程描述了一个在时空自由传播的粒子。我们首次发现的是时空自由传播的马约拉纳粒子的实验证据。后人推广了Majorana的工作,并且讨论了量子Majorana束缚态,其能量严格为零,因此,这种量子束缚态有时也被称为马约拉纳零能模。 在时空自由传播的粒子具有连续能量,并取决于其动量,称为色散关系。 相比之下,量子束缚态被约束在空间某个具体位置,其具有离散的能级。
在我们关于时空自由传播马约拉纳粒子的工作之前,科学界已经对马约拉纳零能模进行了一些实验研究,通常在纳米线的两端实现。马约拉纳零能模的必要但不充分的条件是零能量的量子态。然而,通过实验来证明严格处于零能量是非常困难的。由于有限的能量分辨率,接近零能量的许多平庸状可能被误认为是零能量。更严格的要求是,马约拉纳零能模的数量必须是奇数。如果有偶数个零能模,它们可以成对地相互耦合,其所产生态的能量将不再为零。早期实验确实在零能量附近找到了很宽的电导峰,但是实验不能确定是否存在奇数个零能模,同时峰值也可能由接近零能量的许多其他平庸的态引起。麻省理工学院的李雅达教授和他的同事们给出了一个定量的理论预测,马约拉纳零能模将给出2e2/h的量子化微分电导峰值。在2016年6月2日我们的科学论文提交日期前,所有以前的实验仅达到理论预测的微分电导峰值的1-10%。实验观察的峰值远离理论预言的量子化条件, 说明的确有许多平庸态在零能附近,实验无法分辨在那些平庸态中是否有能量严格等于零的马约拉纳零能模,更无法确认马约拉纳零能模的个数的确是否是奇数。在这个意义上,用微分电导寻找马约拉纳零能模的实验是没有定论的。
另一方面,我们的理论预测手性马约拉纳费米子可以产生1/2 e2/h的量子化电导平台,并且实验测量值接近理论预言的100%。更有趣的是,理论上可以严格证明,手性马约拉纳费米子必然会导致马约拉纳零能模。纳米线实验需要许多微调,如费米能级,模式奇数等。相比之下,量子反常霍尔绝缘体薄膜和超导的耦合体系不需要任何微调,实验证据是清晰的。
以实验精准观察理论预言量子化条件为客观标准,在寻找马约拉纳粒子的竞赛中,我们的团队最先起跑,也是最先到达冲刺线的。而在寻找马约拉纳粒子和马约拉纳零能模的广义竞赛中,我们的团队不是最先起跑的,却是最先到达冲刺线的。
物以稀为贵:手性马约拉纳费米子的特殊性。从狄拉克费米子出发,有两种不同的方法得到狄拉克费米子的一半,一种可以通过手性的条件得到手性或者外尔费米子,另一种则是通过马约拉纳或实数条件。(近年来,在凝聚态物理学中已经发现了手性或者外尔费米子。) 然而,只有在1维空间+1维时间和9维空间 + 1 维时间(它们时间空间维度差8, 体现了深刻的数学概念称之Bott周期)的情况下,可以同时施加手性和马约拉纳条件,以获得手性马约拉纳费米子,这是狄拉克费米子的四分之一。 1维空间+1维时间和9维空间 + 1 维时间的手性马约拉纳费米子是超弦理论的重要组成部分。 超弦扫出1 + 1维的世界面,而它在9 + 1维的时空传播,恰恰是手性马约拉纳费米子存在的两个维度!
► 几种2维拓扑量子态以及它们对应的1+1维边缘态。右下:二维拓扑绝缘体(量子自旋霍尔态),边缘态是狄拉克费米子。右上:量子反常霍尔绝缘体,边缘态是手性狄拉克费米子,自由度是狄拉克费米子的一半。左下:时间反演对称拓扑超导体,边缘态是马约拉纳费米子,自由度是狄拉克费米子的一半。左上:手性拓扑超导体,边缘态是手性马约拉纳费米子,自由度是狄拉克费米子的四分之一。
在凝聚态物理学中,手性马约拉纳费米子也非常特别。 我们可以从二维拓扑绝缘体开始,其边缘态是1 + 1维的狄拉克费米子并呈现出量子自旋霍尔效应。磁性掺杂的拓扑绝缘体导致量子反常霍尔效应,其边缘态为1 + 1维手性费米子,或狄拉克费米子的一半。 量子反常霍尔绝缘体与超导体的近邻效应导致手性拓扑超导体,其边缘状是1 + 1维的手性马约拉纳费米子,其是狄拉克费米子的四分之一。
理论预言了什么?它为什么重要?在2010年至2015年的三篇文章中[1][2][3],我们斯坦福的理论团队预言了在哪里可以找到马约拉纳费米子,以及用什么实验测量迹象来确认是马约拉纳费米子。我们的团队提出手性马约拉纳费米子存在于由量子反常霍尔绝缘体薄膜和常规超导体薄膜组成的混合器件中。随着外磁场的变化,量子反常霍尔绝缘体的电导显示出1和0的量子化平台,以基本常数e2/h为单位,这在以前实验中已经观察到。与传统超导体的近邻效应产生手性马约拉纳费米子,其导致额外的电导平台,为1/2e2/h。由于马约拉纳费米子没有反粒子,在某种意义上说它是常规粒子的一半,因此,额外的半整数量子化平台提供手性马约拉纳费米子存在的明确证据。
按照我们的理论建议,加州大学洛杉矶分校(由王康隆教授领衔),加州大学戴维斯分校(由刘恺教授主持)和加州大学尔湾分校(由夏晶教授主持)的实验家团队与斯坦福大学理论团队密切合作, 在理论建议的器件中发现了手性马约拉纳费米子。 他们在GaAs衬底上制备了量子反常霍尔绝缘体薄膜CrBiSbTe的样品,并由Nb超导体覆盖。 随着扫描外磁场,除了通常的整数量子化平台之外,他们观察到了由我们的理论组预测的半整数量子化平台[4]。 在较高的磁场和三终端进行了额外的实验,令人信服地排除可能的实验假象。
► 左图:我们理论建议实现与测量手性拓扑超导的混合器件,由普通超导覆盖量子反常霍尔绝缘体得到[3]。右图:实验团队制作的手性拓扑超导器件,其中Nb超导体覆盖于CrBiSbTe量子反常霍尔薄膜之上[4]。根据我们理论的预测[3],电极1和2之间的电导会呈现出半整数量子化平台。
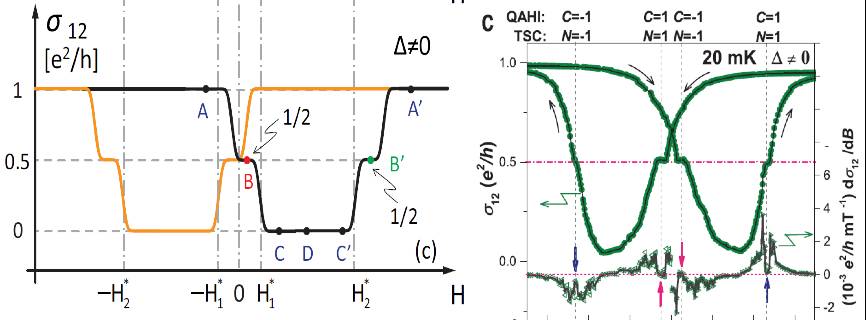
► 左图:我们理论中预测的电导随磁场变化的曲线。其中四个半整数量子化平台标志着手性拓扑超导的出现[3]。右图:实验团队所测量到的电导随磁场变化的曲线与半整数量子化平台,与理论预测相吻合[4]。
著名的科学哲学教授卡尔·波普尔(Karl Popper)表达了这样的观点:科学之所以能区别于伪科学,因为科学能够做出精确的理论预言,并通过实验验证或证否。可验证的理论预言,应该提出精确的器件结构,以便材料科学家相应地生长材料并构建器件。应该预言精确的实验测量,以便在实验中定量测试理论预言。自从我们2006年首次预言了HgTe绝缘体后,在拓扑绝缘体和拓扑超导体领域,理论上预言了几乎所有的材料和效应,都在实验观察之前。理论与实验的定量一致性大大推进了该领域发展。因此,这一领域为物质科学和凝聚态物理学的其他分支树立了榜样,希望有一天我们可以通过理论预测发现有用的材料而造福于人类,并不必用穷举法对每一个可能材料做实验搜寻。
参考文献:
[1] Xiao-Liang Qi, Taylor L. Hughes, Shou-Cheng Zhang, “Chiral Topological Superconductor From the Quantum Hall State”, Phys. Rev. B 82, 184516 (2010).
[2] Suk BumChung, Xiao-Liang Qi, Joseph Maciejko, Shou-Cheng Zhang, “Conductance andnoise signatures of Majorana backscattering”, Phys. Rev. B 83, 100512(R)(2011).
[3] Jing Wang,Quan Zhou, Biao Lian and Shou-Cheng Zhang, “Chiral topological superconductorand half-integer conductance plateau from quantum anomalous Hall plateautransition”, Physical Review B, 92, 064520 (2015).
[4] Qing. LinHe, Lei Pan, Alexander. L Stern, Edward Burks, Xiaoyu Che, Gen Yin, Jing Wang, Biao Lian, Quan Zhou and Eun. Sang Choi, Koichi Murata, Xufeng Kou, TianxiaoNie, Qiming Shao, Yabin Fan, Shou-Cheng Zhang, Kai Liu, Jing Xia and Kang L.Wang, “Chiral Majorana edge modes in a quantum anomalous Hall insulator-superconductor structure”, Science 357, 294 (2017).
加利福尼亚大学洛杉矶分校教授王康隆评论

► 加利福尼亚大学洛杉矶分校教授王康隆。王康隆实验室供图
张老师前3页的稿子,内容是一般科学知识范畴,我并没有意见。但是在“物以稀为贵:手性马约拉纳费米子的特殊性”后,我要澄清以下事实。
首先,对于我们这次发表在《科学》杂志的工作,是一个“实验性”工作(非理论性),张教授并没有参与到我们的实验当中去。实际上,我们文章从2016年6月初投稿到《科学》杂志开始,他并不是这篇论文的“通讯作者”。后来大概是到2017年4月底,他才要求成为文章的通讯作者的。这能很清晰地看出来,他的这篇稿子的后半部分并没有反映整个我们文章工作的真实性,他并没有参与到计划、指导、带领整个实验工作。
我们UCLA团队计划并设计了全部实验流程,包括材料生长、器件制备以及所有的测试表征。首先,我们必须制备出“量子反常霍尔绝缘体”的高质量样品,反复地表现出e2/h的电导量子化现象。这一种样品是花了我们UCLA团队持续13年的材料制备和物性研究积累,方研发而成的。
实际上,早在2003年,我在UCLA成立了一个研究中心,叫FENA(Functional Engineered Nano Architectonics Focus Center),在2005年后,资助了张教授在“量子自旋霍尔效应”的研究。我当时的这一研究计划和资金分配直接导致了2008年末拓扑绝缘体的诞生。值得一提的是,宾州大学的Charles Kane教授在2004年首次在石墨烯上提出了这一概念。
其实,在张教授的这一套理论提出之前,早在2008年,Charles Kane教授和Liang Fu (现于麻省理工学院任教授)后来提出利用拓扑绝缘体和超导体耦合来研究马约拉纳费米子[注]。他们这一概念提出以后,很多相关的理论工作陆续提出并在这一基础上改良。实验上,马约拉纳费米子也已经在早年研究了,包括Delft大学的Kowenhaven教授,普林斯顿大学的Yazdani教授,和上海交大的贾金锋教授等等。同时很多相关的工作还在涌现。张老师在2015年期间理论上提出了另一种结构,但也是基于拓扑绝缘体和超导体耦合来研究马约拉纳费米子的,是对Charles Kane教授的理论的一个改良。我们团队也研究了张老师这一理论文章。
就像其他科研工作一样,我们UCLA团队也需要得到其他团队的帮助和合作,例如,加州大学戴维斯分校的刘凯教授帮我们沉积了超导体薄膜。在测量上,我们首先是去了美国佛罗里达高磁场实验室对马约拉纳费米子样品进行测试的。稍后,为了方便和加快实验进展,我们发现加州大学欧文分校的夏晶教授也有一台同样功能的仪器,于是我们得到夏教授的同意之后,我的学生何庆林和潘磊才前往夏教授实验室进行实验测试的,并得到了他的学生的帮助。
所以我们这一工作,其实和所有的科研一样,我们首先必须研读并参考国际上广泛的已发表的科技论文,从1937年的Majorana的理论工作,到Kowenhaven教授、Charles Kane教授和Liang Fu教授、Yazdani教授、张首晟教授等等,我们都必须从中学习并理解,进而应用到我们实验当中去。我们UCLA团队花费了很多年来研究和提高拓扑绝缘体的样品质量,最终目的就是为了实现我们这一马约拉纳费米子的工作。一般而言,理论能够在某些情况下帮助实验物理学家,另一方面,实验的结果又能促进理论的发展。所以,科学的发展就像一曲交响乐一样。
注:Charles Kane教授和Liang Fu论文可参阅https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.096407
麻省理工学院终身教授、格林讲席教授文小刚评论

► 文小刚于2014年末接受《赛先生》专访。摄影:李晓明
和首晟一样,我一直认为三维的准粒子和三维的基本粒子是没有区别的。我把这一看法概括为信息与物质的统一,或者说物质起源于信息。我认为我们的真空就是由量子信息组成的量子比特海。而我们看到的所谓基本粒子,就是量子比特海中的准粒子。过去十几年,我们做了大量的工作。证明了光波的麦克斯韦尔方程,胶子的杨-米尔斯方程,电子夸克的狄拉克方程,都可以从量子比特海中搞出来,描写其中各种各样不同的波。由此证明了所有基本粒子,都可以看成是量子比特海中的准粒子。这是拓扑序在基本粒子领域中的重大应用。
,以及。
这三篇文章都讲了三维基本粒子就是三维准粒子这一观念。
对于这项新的工作,我此前在接受果壳科学人的采访中做了论述:
之前,人们就已经在有自旋轨道耦合的超导体中发现了以准粒子激发的形式存在的马约拉纳费米子,但当时它被叫做另外一个名字:玻戈留玻夫(Bogoliubov)准粒子。超导体中的准马约拉纳费米子,或玻戈留玻夫准粒子的确和暗物质的一个候选粒子有点像,即自己是自己的反粒子。作为基本粒子的或超导体中的马拉约纳费米子是能在三维跑的。这次的工作发现的是在一维跑的马拉约纳费米子。是很不一样的东西。
我还可以说明一点:
正是因为不一样,所以这一次是一个新工作。1993年我在《物理评论快报》(Physics Review Letters)上发表的文章中,预言了这种一维手征马约拉纳费米子可以出现在非阿贝尔量子霍尔态的边界上。这一类拓扑态有半整数电导。而高精度半整数电导1999年已在量子霍尔试验中被Wei Pan观察到[注]。这间接地发现了一维手征马约拉纳费米子。这次新实验,也是通过半整数电导,间接地发现一维手征马约拉纳费米子。但实验的构造,半整数电导的机制和以前完全不同。
注:Wei Pan的论文Exact Quantization of the Even-Denominator Fractional Quantum Hall State at ν=5/2 Landau Level Filling Factor,Phys. Rev. Lett. 83, 3530 – Published 25 October 1999,DOI:https://doi.org/10.1103/PhysRevLett.83.3530
中国科学院物理研究所研究员戴希评论

► 中国科学院物理研究所研究员戴希。本人供图。
我很赞同首晟的观点,的确基本粒子和准粒子的概念并非绝对的,在一种物质层次下的基本粒子,可以是更微观层次上的准粒子,两者之间存在非常深刻的相似性。这里我想补充一点,其实基本粒子和准粒子的不同,还涉及到自然科学研究中的两种基本思想方法,即还原论和演生论。他们之间并非矛盾和对立的关系,而是看问题视角的不同。还原论的思想方法是把对这一层次的物质运动、演化规律研究分解到下一层次,例如要搞清楚大块物质的物理性质,就要研究组成它的原子、分子,同样要解释原子、分子的特殊性质,就要研究组成它们的电子和原子核,以此类推。还原论认为只要搞清楚了单个基本粒子的运动规律,原则上可以耦合大量类似粒子的运动方程,通过数值计算来预测宏观体系的运动规律。还原论的思想很容易被大众接受,在人类认识自然的进程中曾发挥过重大作用。然而,随着凝聚态物理研究的深入,从上世纪70年代起,人们逐渐认识到,仅仅依靠还原论并不能真正解决由足够大量的“基本粒子”所组成的宏观物质,1972年著名的凝聚态理论物理学家P.W. Anderson在一篇文章中提出“More is different”, 于渌先生把它翻译成“多者异也”,指的就是这个问题。
与还原论相对应的另一种思想方法就是演生论。在演生论中,研究的是大量类似微观客体如何通过微观相互作用,演生出完全不同于微观客体运动规律的,更高物质层次的运动规律。也就是说,演生论强调物质的运动规律是分层次的,在每个层次上都有其独特的物理规律,仅仅搞清楚微观层次的物理规律,对我们理解宏观层次的物理现象还远远不够。
这次实验中发现的一维手征马约拉纳费米子,就是这样一种由相互作用下的电子,在特殊晶格结构下,演生出来的准粒子,其满足的运动方程和统计规律,跟当年马约拉纳假设存在的那种集正/反粒子态于一身的基本粒子,是完全一样的。它们之间的不同之处,正如首晟在文中指出的一样,主要在于能量、长度和时间尺度。
事实上,在极其丰富的凝聚态材料中,如果仅仅找到满足类似某种基本粒子运动方程的准粒子,其科学意义是有限的,更重要的是这些新型准粒子所带来的奇异物理现象,例如外尔费米子和狄拉克费米子态带来的表面费米弧、手性反常和手性磁效应;一维手性边缘电子态导致的整数量子霍尔效应等。这次发现的一维手性马约拉纳费米子,则进一步导致半整数的量子霍尔效应平台,确是一个大的突破。这次实验的重要意义还在于给拓扑量子计算提供了一个全新的材料平台,在其上有可能开展各种拓扑量子计算领域期待已久的实验工作,非常值得期待。
本文由微信公众号“知识分子”(ID:The-Intellectual)授权转载
编辑:huashan